第 24 讲 再论仿真世界: 森林里有几只老鼠,几只猫头鹰?
一、实验目的
森林里有繁殖能力超强的老鼠,还有专门吃老鼠的猫头鹰。像图 24-1 中 显示的那样,老鼠多了,猫头鹰有了食物,也会变多;猫头鹰一多,吃的老鼠 也多,老鼠反而会变少,猫头鹰缺少食物会被饿死;猫头鹰少了,老鼠又会变 多……哎呀,好复杂!
那森林里到底有几只老鼠,几只猫头鹰呢?想是想不清楚了,我们写个程 序模拟一下,看看老鼠和猫头鹰的数量变化吧!
二、背景知识
假设远古时代,黑暗森林纪元元年,森林里有 10 万只猫头鹰,100 万只老鼠。老鼠和猫头鹰的出生率和死亡率如下:
● 老鼠:繁殖能力超强,第 2 年的数量是第 1 年的 1.1 倍,变成了 100× 1.1=110 万只。不过老鼠也有一定的死亡率,因为每 1 万只猫头鹰会吃 掉 0.2 万只老鼠,10 万只猫头鹰会吃掉 10×0.2,即 2 万只老鼠。因此 第 2 年共有 118 万只老鼠。
● 猫头鹰:寿命不长,死亡率超级高,第 2 年的数量是第 1 年的 0.4,就 是变成了 10×0.4=4 万只,但是如果猫头鹰有足够的老鼠当食物的话, 会生小猫头鹰,小猫头鹰数量是老鼠数量的 0.3,就是 100×0.3,即 30 万只,这样第 2 年共有 34 万只猫头鹰。
这样一直进行下去,会发生什么事情呢?猫头鹰多还是老鼠多?包若宁的 猜测是:猫头鹰的死亡率是 60%,森林里应该很快会没有猫头鹰了啊。傅鼎 荃的猜测是:猫头鹰少→老鼠多→猫头鹰多→老鼠少→猫头鹰少,那应该是个
“一年多,一年少”的循环啊? 真是“公说公有理,婆说婆有理”,到底谁说的对呢?我们写个程序当裁 判吧!
三、基本思路
我们设置两个列表,分别记录老鼠和猫头鹰历年的数量,然后依据今年的 猫头鹰和老鼠的数量估计明年猫头鹰和老鼠的数量。比如:
(1)第一年:
● 老鼠有 100 万只
● 猫头鹰有 10 万只
(2)第二年:
● 老鼠的数量 =(100×1.1) - (10×0.2) = 110-2 = 108(万只)
● 猫头鹰的数量 =(10×0.4) + (100×0.3) = 34(万只)
(3)第三年:
● 老鼠的数量 =(108×1.1) - (34×0.2) = 118.8 - 6.8 = 112(万只)
● 猫头鹰的数量 = (34×0.4) + (108×0.3) = 46(万只) (4)其他年份的依次类推。
角色设计
● Rat:老鼠。
● Owl:猫头鹰。
● Cat:森林之王,统计森林里动物的数量。
过程描述
(1)猫头鹰的脚本
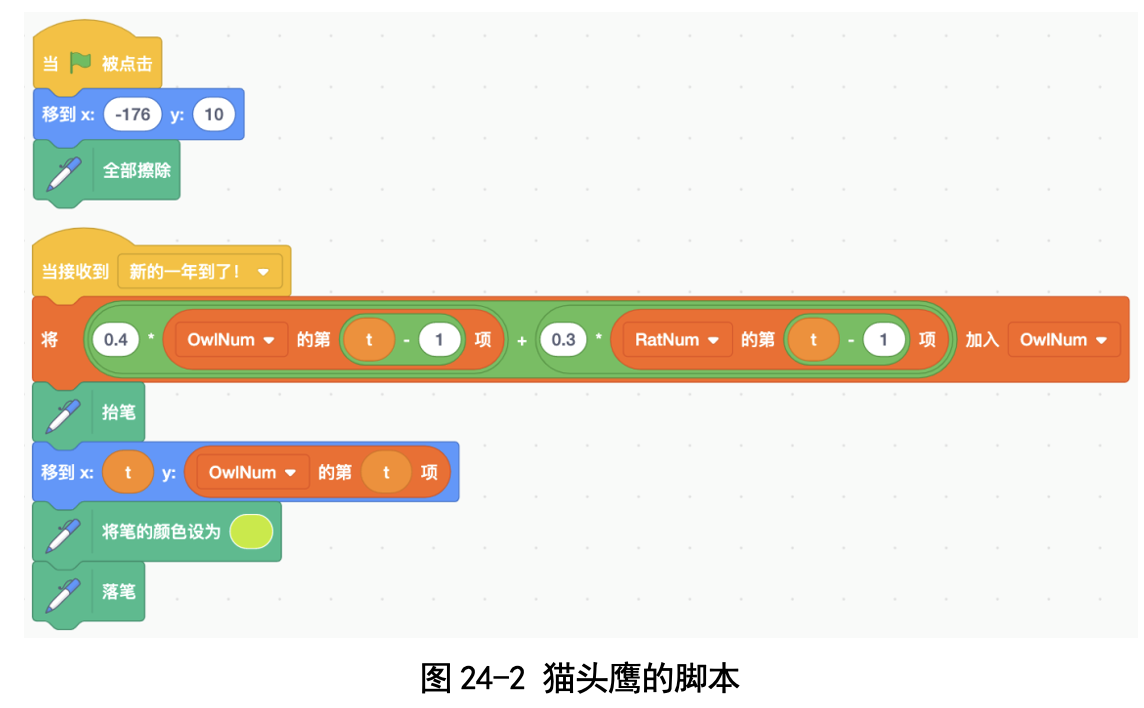
猫头鹰收到森林之王发来的“新的一年到了”消息之后,根据上一年猫头 鹰和老鼠的数量,计算今年会有多少只猫头鹰(见图 24-2)。
(2)老鼠的脚本
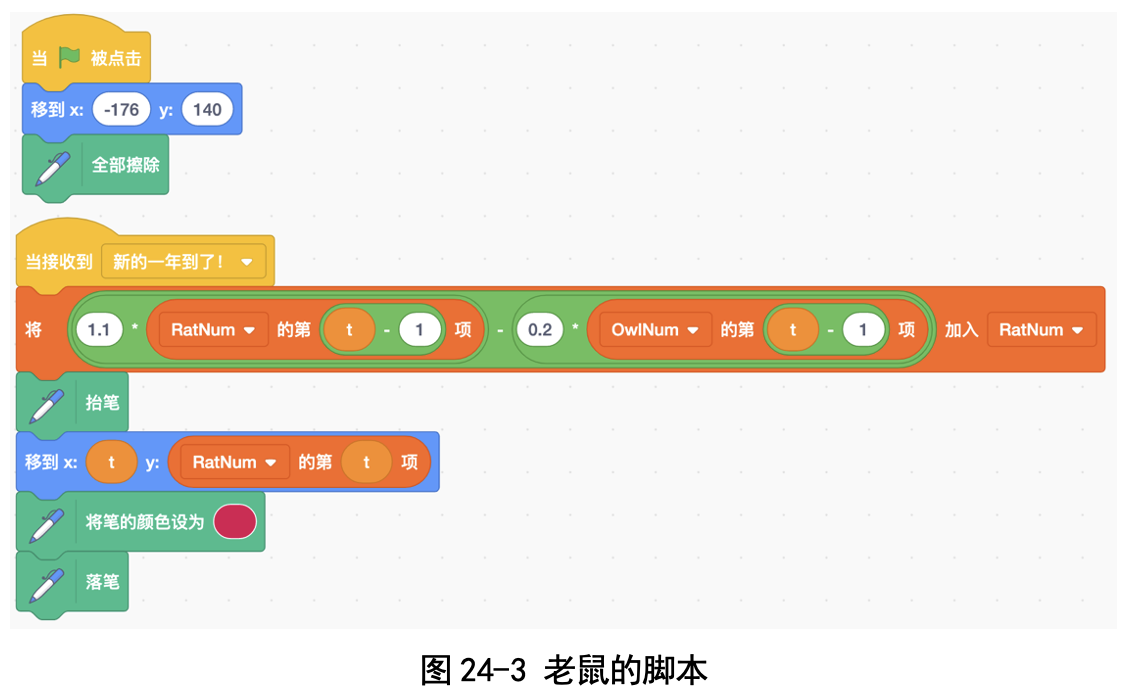
老鼠收到“新的一年到了”消息之后,根据上一年猫头鹰和老鼠的数量, 计算今年会有多少只老鼠(见图 24-3)。
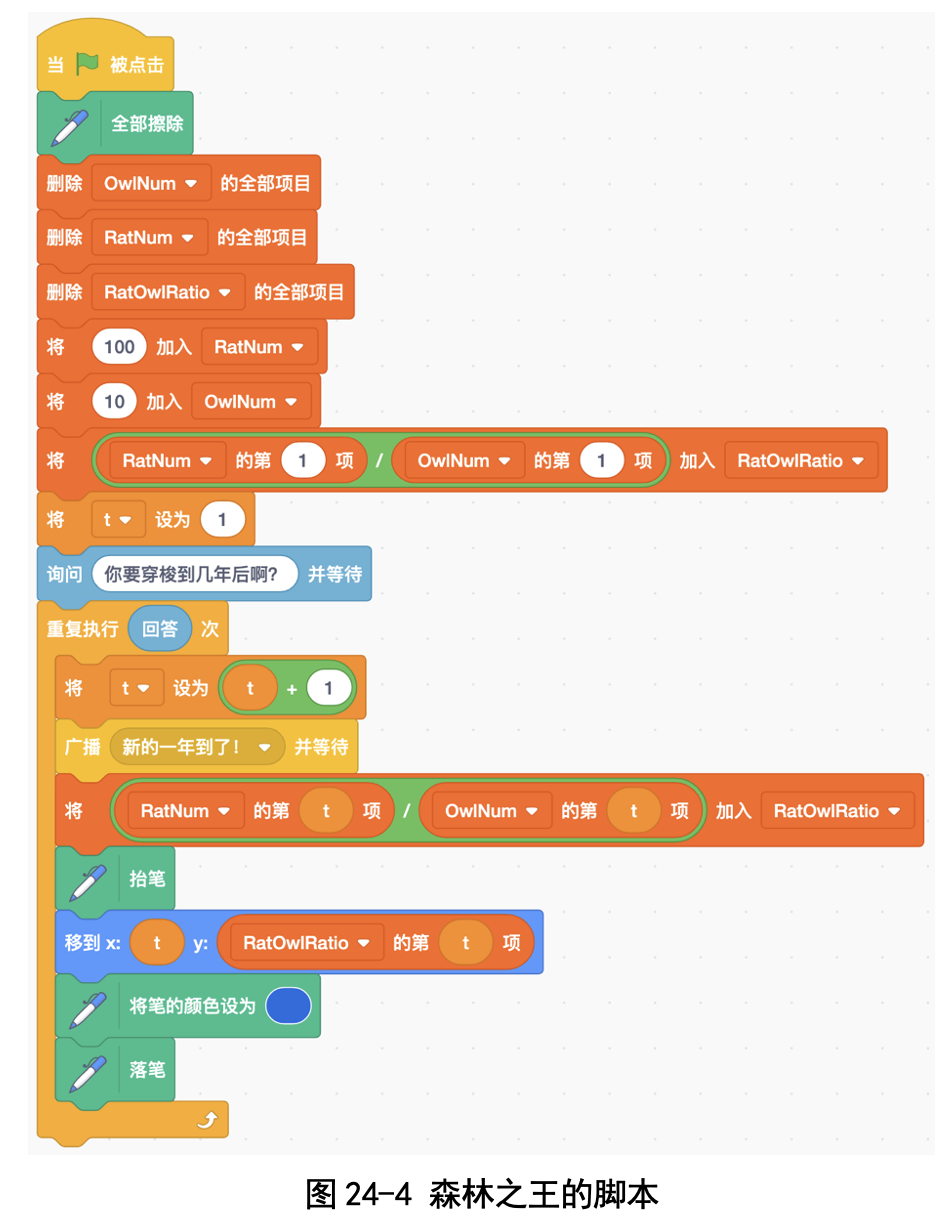
(3)森林之王的脚本 森林之王一开始设置森林里有 100 万只老鼠和 10 万只猫头鹰,然后广播 “新的一年开始了”消息,等待老鼠和猫头鹰接收到消息之后更新数量,然后 计算两者数量之比,绘图(见图 24-4)。
代码下载及Web版
点击森林里猫头鹰和老鼠数量仿真的代码下载于本地运行,或点击森林里猫头鹰和老鼠数量仿真程序Web版直接运行
国内用户如果无法访问scratch.mit.edu的话,请点击国内可访问的Web版直接运行
六、实验结果
从图 24-5 所示的变化曲线,我们可以观察到这样的现象:
● 猫头鹰的数量:猫头鹰的数量从 10 万只开始逐渐增大,从第 10 年就稳 定下来,不再变化了,保持在 58 万只。
● 老鼠的数量:和猫头鹰的数量变化类似,老鼠的数量也是从 100 万只逐 渐增大,到 46 年的时候就已经平稳不变了,保持在 116 万只。
● 猫头鹰和老鼠的数量之比:老鼠数量增长,猫头鹰数量也增长,最后都 稳定下来了。老鼠和猫头鹰的数量之比一开始比较大,是 10,然后迅速 下降,等到第 10 年的时候,就下降到了 2 附近,再之后就基本不变了。 数量和比例都稳定下来了,我想这就是自然界的规律吧。

七、思考与延伸
(一)要是第一年只有 50 万只老鼠呢?
刚才是第一年有 100 万只老鼠、10 万只猫头鹰的情况,最后都稳定了。 要是一开始只有 50 万只老鼠呢?我们几个人各自运行自己的程序,得到的结 果如表 24-1 所示。
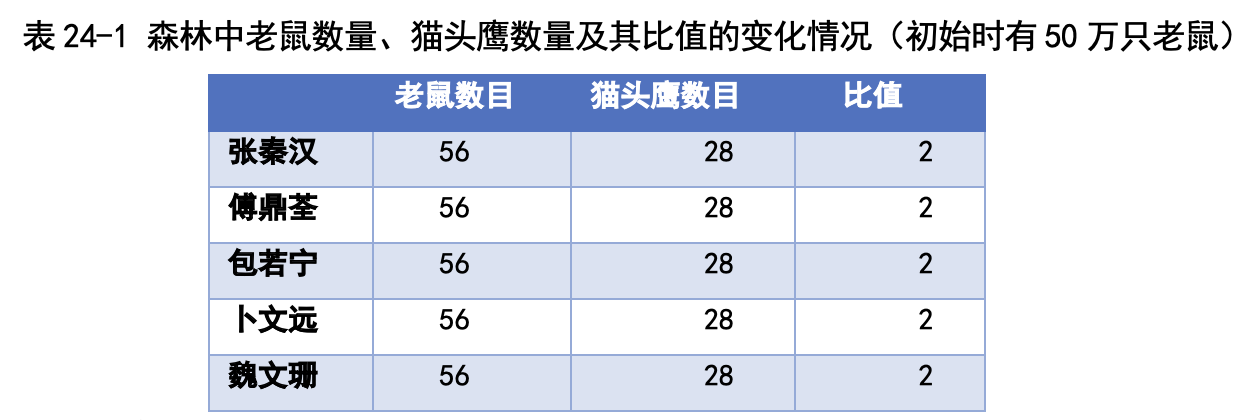
我们四个人得到的结果都一样:老鼠数量稳定在 56 万只,猫头鹰数量是 28 万只,比值还是 2,跟第一年 100 万只老鼠的时候一模一样。
(二)假如 1 万只猫头鹰每年吃掉 0.1 万只老鼠呢?
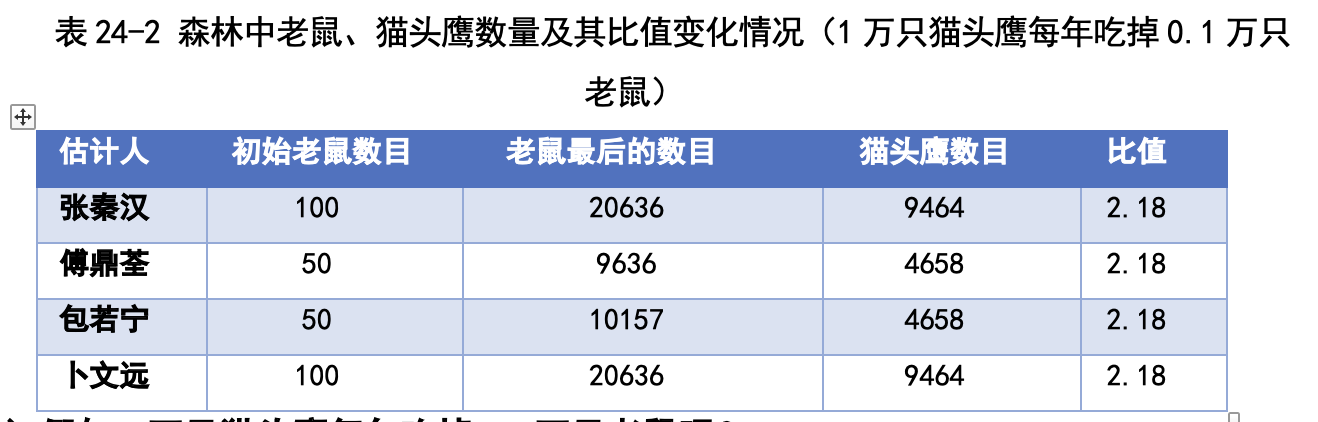
刚才我们假设 1 万只猫头鹰每年吃掉 0.3 万只老鼠,要是猫头鹰吃得少一 点,每年吃掉 0.1 万只老鼠呢?我们模拟的结果如表 24-2 所示。
我们可以看出,虽然初始的老鼠数量不同,但是最后得到的比值都是一样 的,而且和上面两种情况是差不多的,是 2.18,只差了 0.18.
(三)假如 1 万只猫头鹰每年吃掉 0.2 万只老鼠呢?
从模拟结果我们可以看出,猫头鹰数目都是 0.1008,老鼠数目也差不多都 是 0.057,比值都是 1.767。
看来猫头鹰的饭量越大,最后老鼠跟猫头鹰数量的比值越小,这个倒是正 常的。不过当猫头鹰的饭量是 0.2 的时候,最终的比例虽然稳定,但是无论是 老鼠还是猫头鹰都很少,快灭绝了(见表 24-3)。
当然,我们还可以改变老鼠、猫头鹰的繁殖速度,看看会发生什么情况; 或许傅鼎荃猜测的“一年大、一年小”的情况会发生呢!

八、教师点评
森林里的老鼠和猫头鹰是一个典型的“猎物 - 捕食者”动力学系统。孩子 们目前当然不必知道“动力学”这样高深的名词,只需要知道“从上一年的数 量能够算出下一年的数量”就足够了。
孩子们变换不同的参数,观察到这样的现象:老鼠、猫头鹰的数量之比和 第一年的数量是没有关系的,只跟老鼠、猫头鹰的繁殖率,以及它们之间的捕食有关系。 孩子们做的实验里,老鼠、猫头鹰的数量之比最终都会稳定下来,那会不 会出现傅鼎荃猜想的“一年大、一年小”这种波浪形呢?会的!我们改变老鼠 的繁殖率,是会观察到这种现象的。 一个有名的案例,就是卢卡斯书中写的加拿大山猫 - 雪兔的数量变化,的确是周期性的。
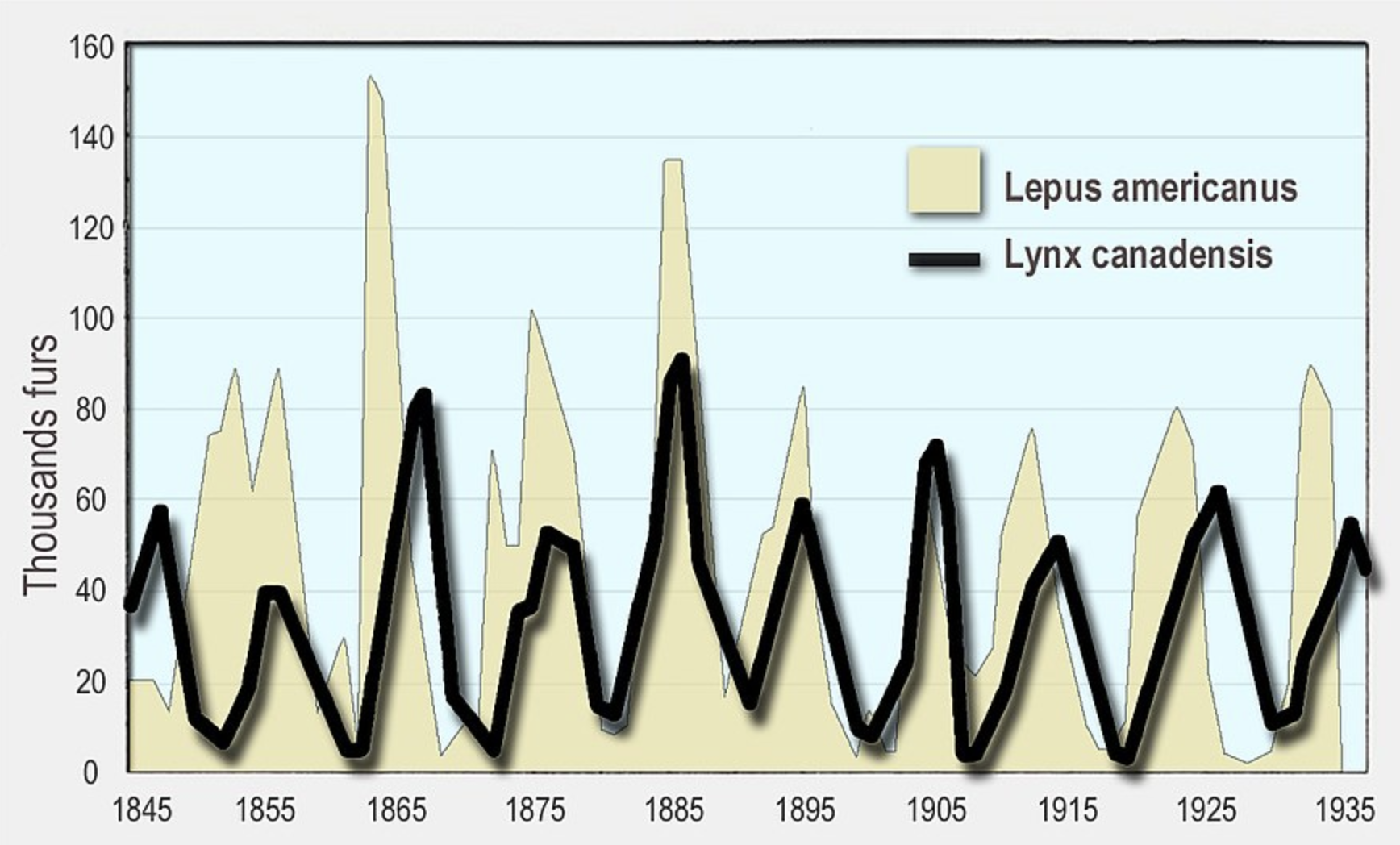
图24-5 加拿大山猫-雪兔数量周期性变换。图片源自 https://upload.wikimedia.org/wikipedia/commons/thumb/5/5b/Milliers_fourrures_vendues_en_environ_90_ans_odum_1953_en.jpg/880px-Milliers_fourrures_vendues_en_environ_90_ans_odum_1953_en.jpg
美国 C. Lay 教授写的名著《线性代数及其应用》里讲到矩阵特征值时, 就是用的老鼠 - 猫头鹰这个捕食系统作为第一个例子。张秦汉小朋友对“猫头 鹰 - 老鼠”这个问题非常感兴趣,一直想弄明白为什么最后会稳定,什么时候 才会“一年大、一年小”。这些问题留给他以后去证明吧。