第 23 讲 仿真世界:牛顿的大炮
一、实验目的
牛顿在他的一本书里提出过一个有趣的问题:把一门大炮搬到山顶上,水 平发射炮弹,那炮弹会怎样飞呢?
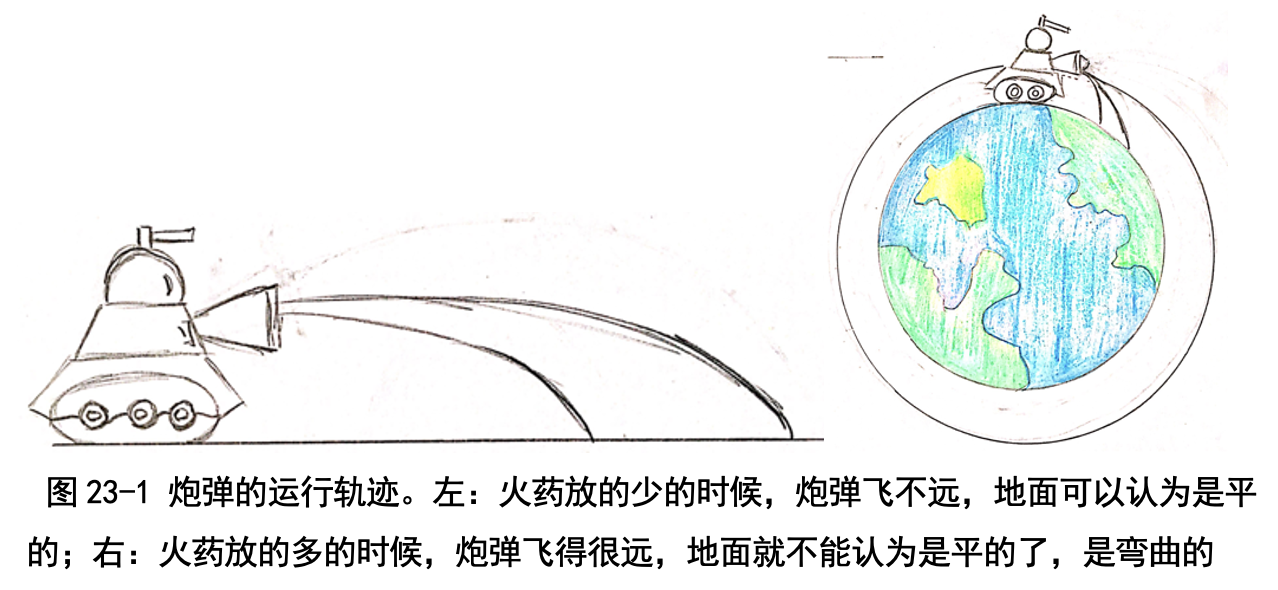
如果没有地球对炮弹的引力的话,炮弹会一直水平飞。当然我们知道这是错 的:地球对炮弹有引力,会拉着炮弹向下拐弯,一会儿就落地了(见图 23-1)。 不过牛顿想得更多一点:要是炮弹里的火药装多一些,炮弹飞得再快一点, 那会怎样呢?我也不知道,咱们一起编程模拟一下吧!
二、背景知识
(一)牛顿是谁?

第一次听到牛顿的名字,我还以为他姓牛呢!后来才知道他不姓牛,而是姓牛顿,名字叫艾萨克,全名是艾萨克·牛顿(Issac Newton)。 关于牛顿有很多传说:比如被苹果砸到脑袋,发现了万有引力定律(卜老师告诉我们此事真假存疑,部分来源于伏尔泰的转述);还有就是牛顿用三棱 镜把一束白光分解成多种颜色的光,再用一个三棱镜又混成了白光。
牛顿真是牛啊!
(二)牛顿的大炮是用来做什么的?
牛顿想用“山顶上开炮”实验说明“炮弹飞快了就是一颗小行星”,以此 来说明他的引力理论既适用于炮弹,也适用于行星,是个“万有引力”理论。
按照通常的想法,水平开炮,炮弹被地球吸引,会拐弯,一会儿就会落 地;不过牛顿想得更多:多装火药,炮弹就飞得远一点才落地。 要是再多装一些火药呢?一个关键的问题出现了:大地可不是平的,而是 向下弯曲的;地球地球,地面可是一个弯曲的球面啊。那么炮弹往下拐弯的同 时,大地也往下弯曲,那炮弹可能永远都不会碰到地面(见图 23-1)。岂不是 炮弹就成了一颗环绕地球一直飞的卫星呢?
这就是牛顿当时的想法。不过具体装多少火药,也就是炮弹的速度是多少 才能变成卫星(第一宇宙速度,即 7.9 km/s),咱们写程序模拟一下看。
三、基本思路
如何模拟炮弹的轨迹呢?
炮弹一开始发出来是沿着水平方向走的,但沿着水平方向走的只是刚发出 来的那一刻,下一刻就会向下坠一点点。这是很细微的变化,我们看不见,不 过用不了几秒,就会发现炮弹已经拐弯向下走了。
地球对炮弹的引力会改变炮弹的速度。这很好理解:我骑自行车的时候, 同学拉着自行车,我的速度就变慢了,要是向前拉,我就骑得越来越快。
引力一开始改变炮弹垂直方向的速度,垂直方向的速度改变炮弹的 y 坐标;引力也会改变炮弹水平方向的速度,水平方向的速度改变炮弹的 x 坐标。 概括一下:“引力改速度,速度改位置。”
变量设计
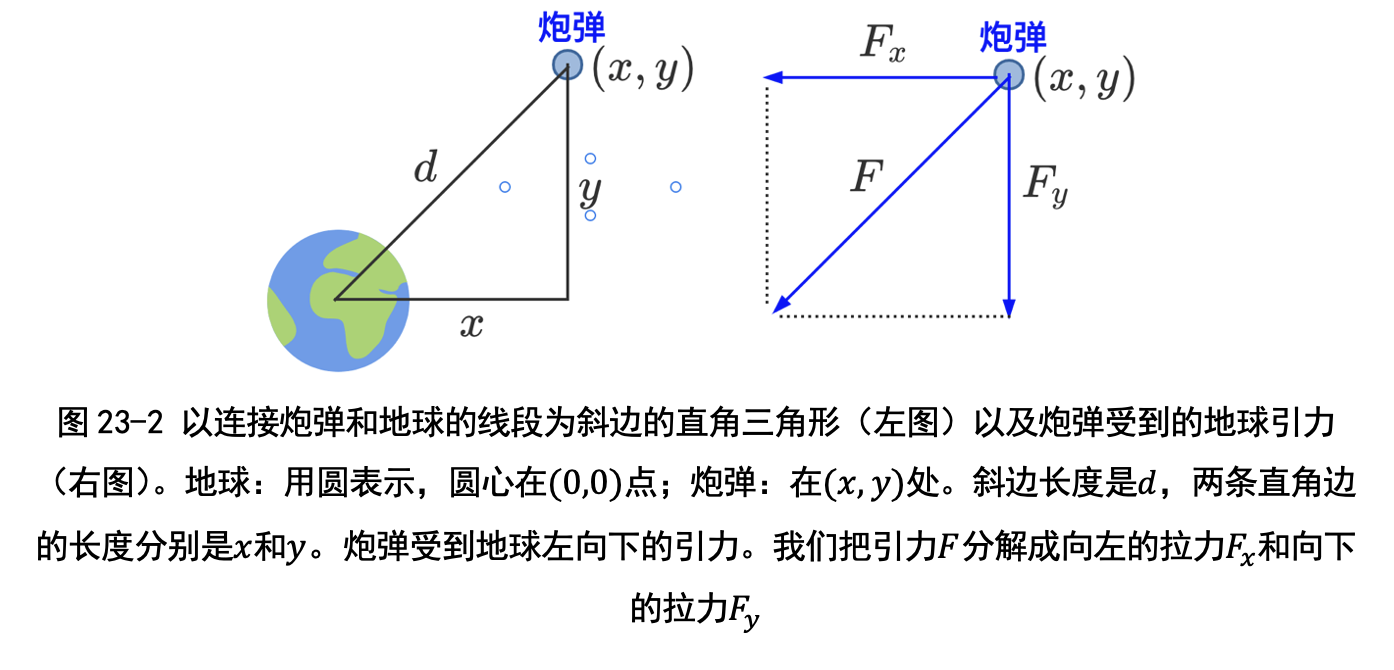
(1)位置:我们用 (x, y) 表示炮弹的位置;用 d 表示炮弹到地球的距离(见 图 23-2 左图)
(2)引力:用 F 表示地球对炮弹的引力(也叫万有引力);用 Fx 和 Fy 分别 表示水平方向的力和垂直方向的力(见图 23-2 右图)。
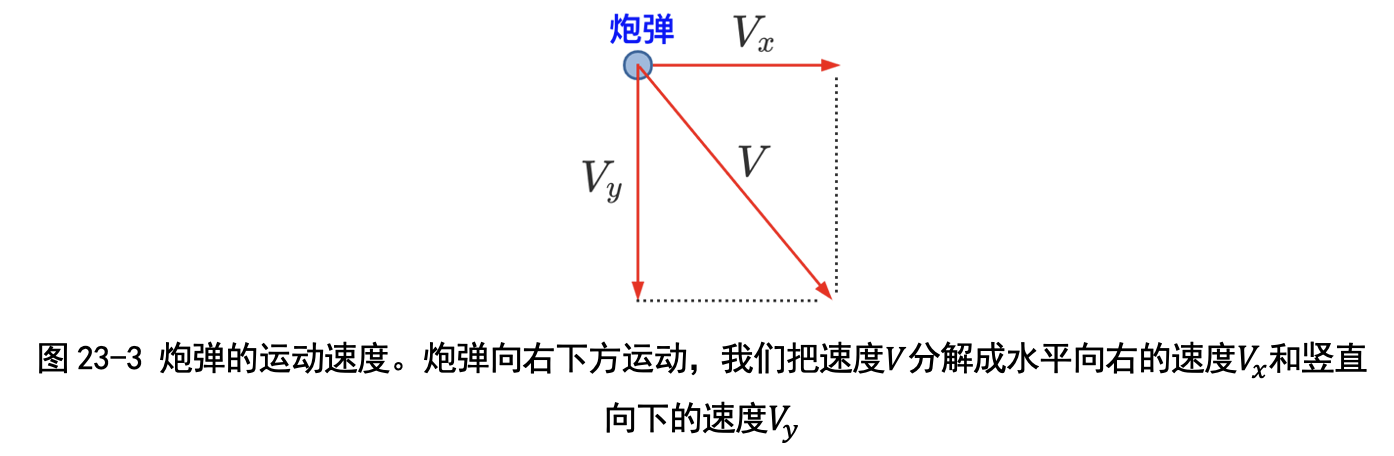
(3)速度:我们用 Vx 和 Vy 分别表示炮弹水平方向和垂直方向的速度(见 图 23-3)
那引力有多大呢?牛顿的万有引力定律说“距离越大,引力越小;引力和距离的平方成反比”,也就是说 F = 1/(dxd) 。(卜老师说这个公式是简化后的公式:引力和地球、炮弹的质量有关;这里地球和炮弹的质量一直不变,我们就省略了。)不过炮弹受到的拉力 F 是斜着的,那水平方向拉力 Fx 和垂直方向拉力 Fy 又是多少呢?
为了弄明白这一点,卜老师带着我们用三个弹簧秤做了一个小实验:一 个弹簧秤斜着拉,一个弹簧秤沿着水平方向拉,另一个弹簧秤沿着竖直方向 拉(具体的实验过程见后面的“教师点评”)。实验结果表明:炮弹受到斜方向 的拉力 F 和水平方向的拉力 Fx、垂直方向的拉力 Fy 组成一个直角三角形(见 图 23-3)。按照比例关系,我们这样计算水平方向的拉力 Fx 和垂直方向的拉力 Fy:
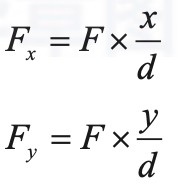
过程描述
我们总结一下上面的分析:每过一秒,炮弹的位置 (x, y) 都会改变;改变 多少是由水平速度 Vx 和垂直方向速度 Vy 决定的。
● 新的 x = 原来的 x+Vx×1
● 新的 y = 原来的 y+Vy×1
每过一秒,炮弹的速度也会发生改变;改变多少是由受到的引力决定的:
● 新的 Vx = 原来的 Vx+Fx×1
● 新的 Vy = 原来的 Vy + Fy×1
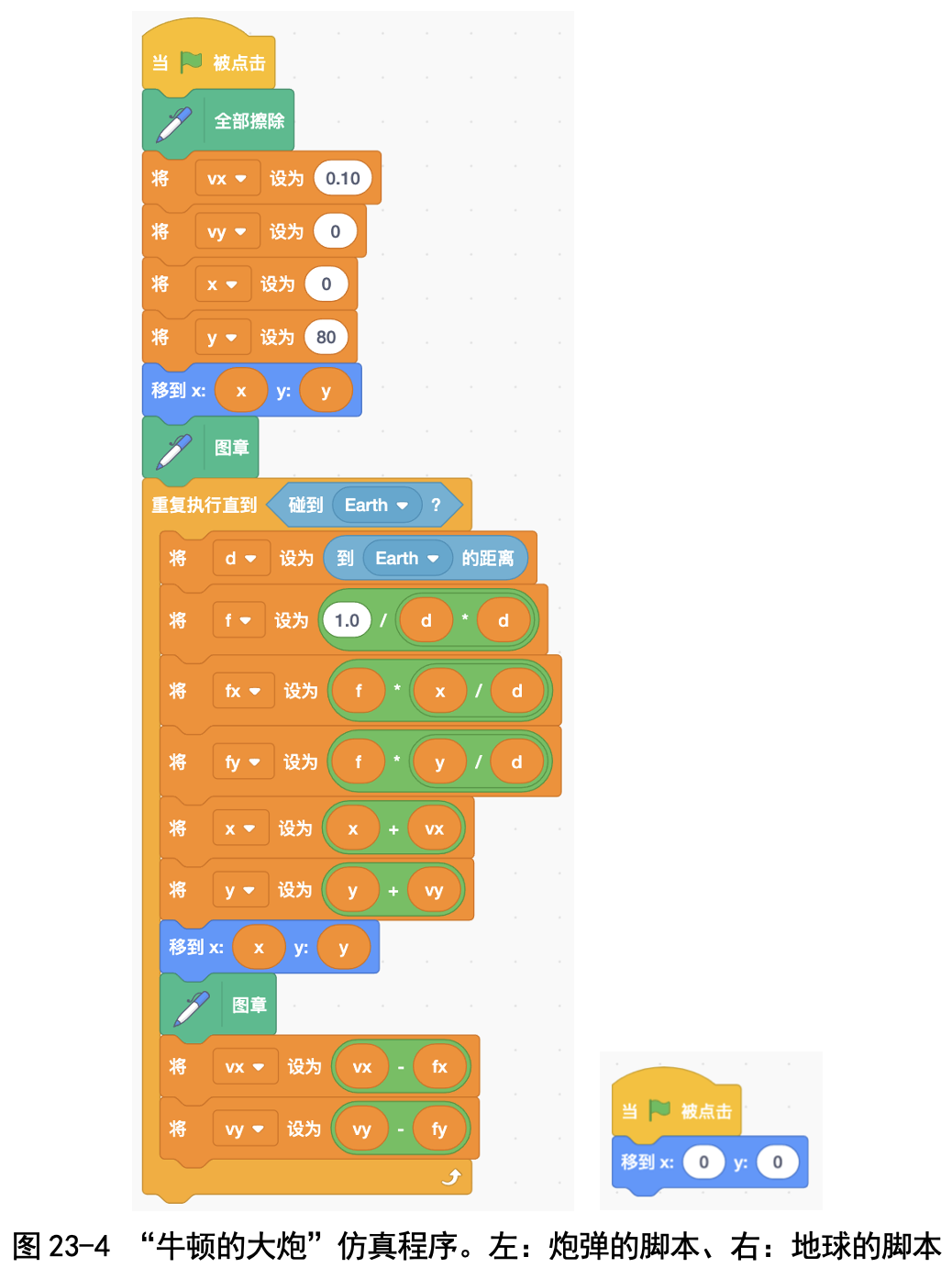
如图 23-4 所示,炮弹的仿真程序就是在不断重复这两个过程:每一秒重 新计算一下水平方向的拉力 Fx 和垂直方向的拉力 Fy,然后用上面的式子计算 新的水平速度 Vx 和垂直方向速度 Vy ,最后再计算新的位置 (x, y),移动到新位 置之后盖个章就行了。
代码下载及Web版
点击牛顿的大炮仿真程序下载于本地运行,或点击牛顿的大炮Web版直接运行
国内用户如果无法访问scratch.mit.edu的话,请点击国内可访问的Web版直接运行
六、实验结果
现在我们运行一下程序,看看随着火药不断增加,速度变大,炮弹轨迹如何变化吧。图 23-5 显示这个仿真程序的运行结果:
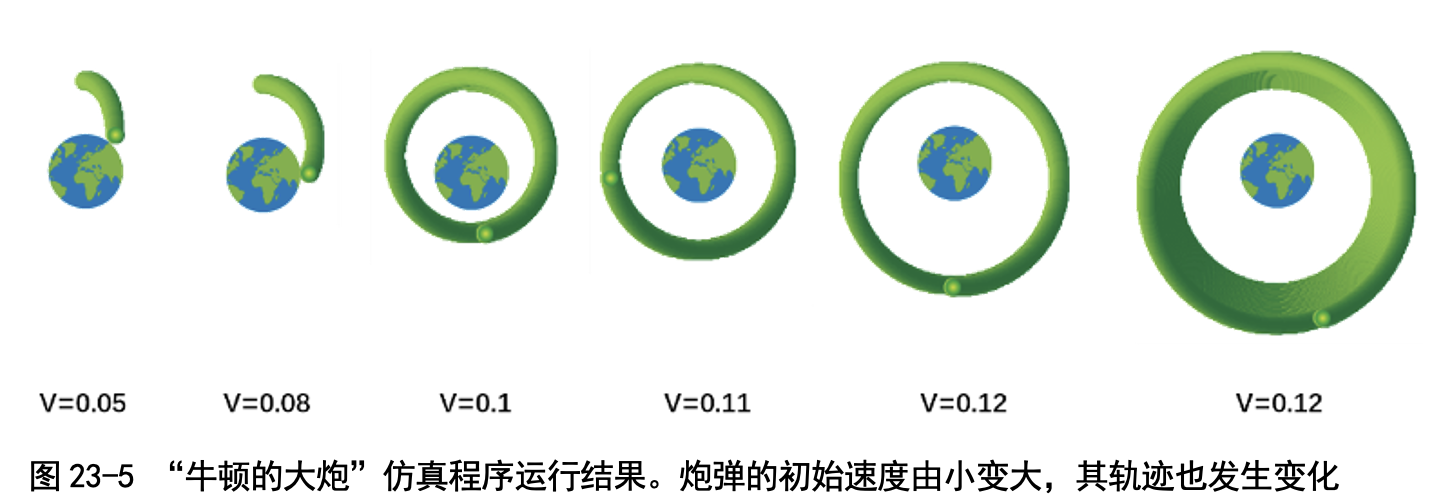
1)当炮弹速度等于 0.05 时,轨迹是抛物线,一会儿就落地了。
2)当炮弹速度等于 0.08 时,轨迹还是抛物线,就是走的距离更远了。
3)当炮弹速度等于 0.1 时,轨迹是椭圆;炮弹弯,地面也弯,炮弹不落 地,成卫星啦!
4)当炮弹速度等于 0.11 时,轨迹成了圆形,地球是圆心;这是一颗地球 同步卫星。
5)当炮弹速度大于 0.12 时,轨迹又变成了椭圆。不过跟上一次的椭圆不 同,这次地球偏在椭圆的上半部分。
6)我多运行一会儿,结果发现这个椭圆竟然不断往外扩散,很奇怪!卜 老师说这应该是 Scratch 计算的误差;当炮弹发射时,时刻都有引力的作用, 不会向外扩散。
七、思考与延伸
其实牛顿并没有拿着大炮去发射,而是在头脑中思考,这样的实验叫“思 想实验”。
如果速度一直增大,大炮有可能冲出地球走向太阳系(必须达到宇宙第 二速度,即 11.2km/s);如果再增大将冲出太阳系走向银河系(宇宙第三速度, 即 16.7km/s);如果再增大将会冲出银河系,炮弹不知道绕着哪个星系转了。 炮弹在宇宙中乱撞,可就出大事了!如果我们能掌握好发射的力量和角度,它 就不会在宇宙中乱撞了,会飞到我们指定的行星去做卫星。
不过引力到底是怎样形成的呢?要是能够设计一种地毯,隔绝重力对我的 吸引,我把一路都铺上毯子,就能飞去学校了,那该多好啊!
八、教师点评
“牛顿的大炮”是一个思想实验。牛顿自己并没有带着大炮去山顶开炮; 孩子们写程序来仿真,也是一种思想实验。在实验中观察到抛物线先变成椭 圆,再变成圆,最后又变成椭圆,孩子们非常兴奋!
在这个实验里,关键之一是“当引力 F 是斜方向的时候,在水平方向的分 量 Fx 和垂直方向的分量 Fy 分别是多少呢?”为了避免引入“分量”这些概念, 我们带着孩子们用三根弹簧秤做了个补充实验,终于从直观上弄明白了这个 问题!
孩子们对引力非常好奇,也有一些自发的思考;可见好奇心是自发萌生的, 有时都不用诱导。比如卜文远同学,上三年级的时候就问过“引力怎么来的? 能否隔开?为何隔不开?”,甚至还想发明一种“能够隔绝重力的飞行毯”。
这些问题我回答不了,现有的物理学知识还解释不清楚引力的来源。 在这一讲,我们还给孩子们补充了以下的知识点。
(一)如何根据斜方向的拉力 F 计算出水平方向的拉力 Fx 和竖直方向的拉力 Fy ?
在这个实验里,关键之一是“当引力 F 是斜方向的时候,在水平方向的分 量 Fx 和垂直方向的分量 Fy 分别是多少呢?”为了避免引入“分量”这些概念, 我们带着孩子们用三根弹簧秤做了个补充实验,终于从直观上弄明白了这个 问题!
做这个实验时,我们让三位小朋友各拉一根弹簧秤:一个弹簧秤斜着拉, 模拟地球对炮弹的引力 F ;另外两个弹簧秤分别沿着水平方向和垂直方向拉, 分别模拟 Fx 和 Fy。孩子们使劲儿拉,还得注意保持钩子交叉点稳定在原点、 两个弹簧秤要处于水平和垂直方向。
图 23-6 显示一次实验的结果:斜方向、水平方向和垂直方向的弹簧秤读 数分别是 F=4.190, Fx=2.485, Fy =3.015。不过直接从这些读数上看不出什么规 律,这是因为我们买的弹簧秤精度比较差:两个弹簧秤对头拉,读数竟然不 一样!
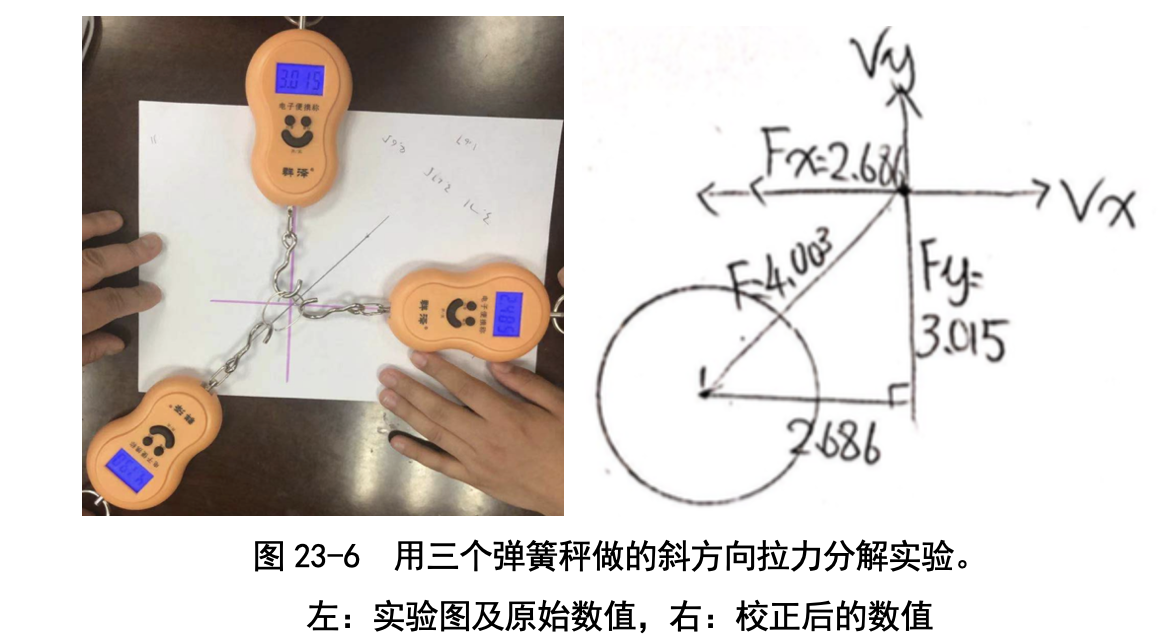
我们只好以水平方向的弹簧秤为基准,重新校准了一下另外两个弹簧秤,得 到了新的数值:F=4.003, Fx=2.686, Fy=3.015。卜文远同学画了一幅图(图 23-6 右图),这回就看出来规律啦!
2.686x2.686 + 3.015x3.015 = 4.003x4.003 ≈ 16.024
用符号表示,就是
Fx的平方 + Fy的平方 = F的平方
这一下子,孩子们立刻就兴奋了:这就是勾股定理啊,那肯定是直角三角形啊!
当然了,后面还得说明由力 F, Fx, Fy 组成的直角三角形与由距离组成的直 角三角形相似。这超出了孩子们的知识范畴和我们用的弹簧秤的精度,我只能 直接提这个结论,没法给出更好的论据来。
(二)平方反比率的推导和背后原因
详细内容请参见书中第23讲。
(三)牛顿和他所在的那个光辉时代
非常需要给孩子们补充的,是一些科学史:牛顿出生于 1643 年;在牛顿 出生的前一年,另一位大物理学家伽利略去世,有点儿牛顿接伽利略的班儿的 意思。伽利略可不简单:他摒弃了亚里士多德的“纯粹思辨”研究方法、倡导 “靠观察和实验”的科学研究方法,因此被称为“现代科学之父”。
按照日本物理学家朝永振一郎的主张:现代科学的出现,可以开普勒在 1618 年提出天体运行三定律为标志,到现在也只有 400 年多一点。牛顿出生 的第二年,恰好是清兵入关、明朝灭亡。看来现代科学的萌芽,确实是在明末 清初,也只有 400 多年的历史啊!
(四)用更大号的三棱镜重做牛顿的光谱实验
牛顿用三棱镜把白光分解成光谱。不过牛顿用的三棱镜小了点,如果用更 大号的三棱镜会出现什么情况呢?物理学家夫琅禾费使用大号的三棱镜,把太 阳光分解成更清晰的光谱,结果观察到彩色光谱中会有一些黑色的暗谱线;后 来发现这些谱线和太阳表层和地球大气层中的元素相关。
希望孩子们长大后学习到量子力学时,能够想起“大号的三棱镜”来。