第 22 讲 “二分法”的应用:估计√2的值
一、实验目的
学完勾股定理之后,我们大家都知道对于边长为 1 的正方形来说,对角线的长度是根号2 。这里根号2是指这样一个数:它自己乘以自己,乘积是 2。 那√2到底是多少呢?我用圆规转一下,发现 √2会落在 1 和 2 之间(见 图 22-1),也就是比 1 大、比 2 小。我又画了一个边长为 1cm 的正方形,用尺 子量一下对角线,估计长度是 1.4cm,也就是说, √2大约等于 1.4。
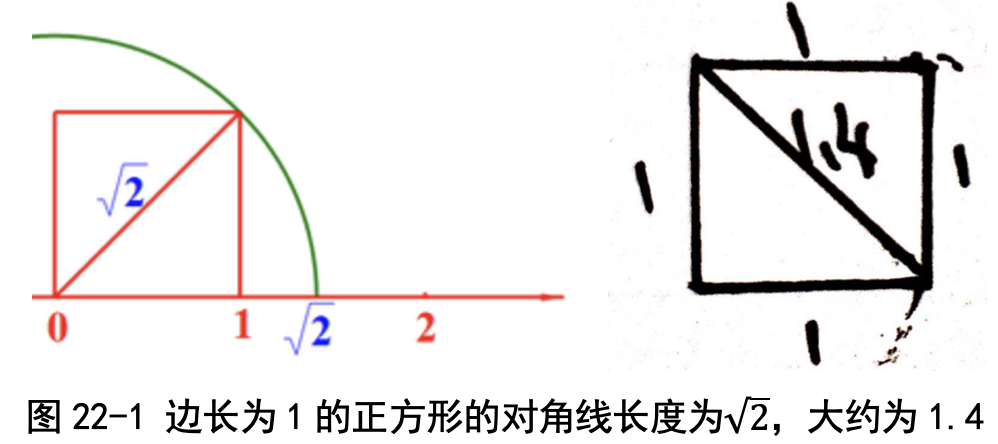
那么能不能想个办法,把√2估计得更准确一些呢?我们只学过加减乘除, 开平方没学过啊,那√2可怎么算?
不要担心,平方根这种“逆向”运算我们不 会,可是“正向”的平方我们会算啊。我们可以先猜测根号2的一个估计值,然后进 行正向运算,看看估计值的平方是比 2 大还是比 2 小呢?如果估计值大就减少 一点,小就增大一点。这样不断调整估计值,很快就估计得越来越接近根号2了。
来,我们一起写一个程序估计一下√2吧。
二、背景知识
(一) √2是怎么发现的?
毕达哥拉斯(Pythacoras of Samos,公元前 570 年— 前 495 年)的一位 学生叫希帕索斯,他发现边长为 1 的正方形其对角线长度不是整数,也不能用 分数表示,所以只能创造出一个新的数来表示,这个数就是√2。
(二)毕达哥拉斯是谁?
毕达哥拉斯是一名古希腊哲学家、数学家和音乐理论家,和我国的孔子是 同时代的人。和孔子一样,毕达哥拉斯也收了很多学生,形成了一个学派,这 个学派证明了毕达哥拉斯定理:直角三角形两直角边长度的平方之和等于斜边 长度的平方,也就是中国古代的“勾股定理”。毕达哥拉斯是用了 4 个直角三角形,摆成两种正方形来证明的(见图 22-2)。
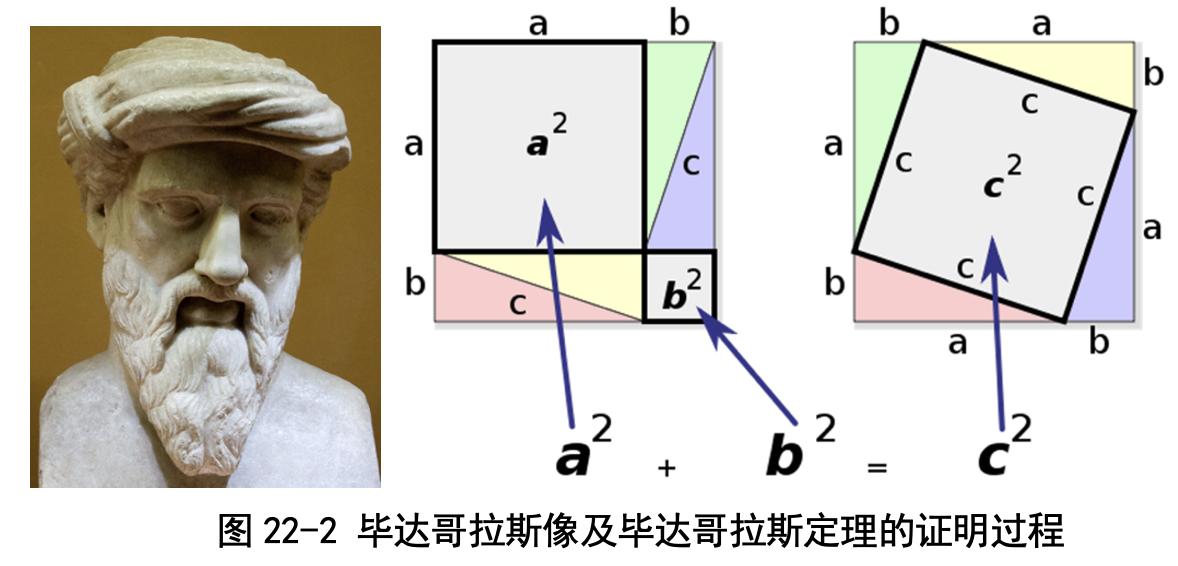
据说证明了这个定理之后,毕达哥拉斯非常高兴,杀了 100 头牛庆祝,所 以这个定理又称为“百牛定理”。
(三)为什么说√2的发现是一件重要的事情?
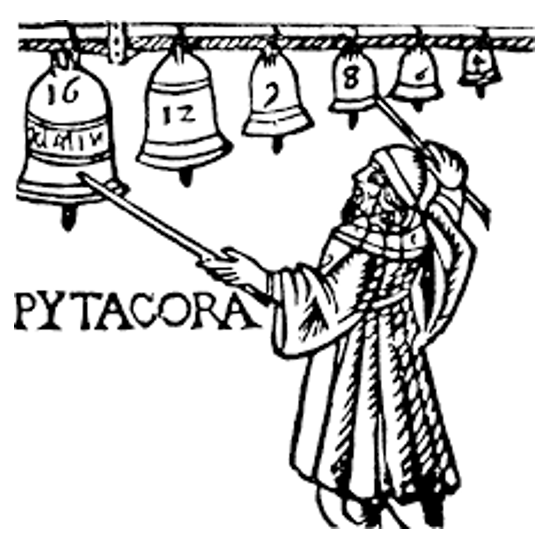
毕达哥拉斯学派信奉“万物皆数”,就是世上万 物都能用“整数或整数之比”来表示。
为什么毕达哥拉斯认为整数及整数之比那么重 要呢?有一个小故事能够说明:相传毕达哥拉斯路 过铁匠铺,觉得打铁时大锤和小锤的敲击声特别和 谐,原来大锤小锤的重量之比恰好是特定整数之比, 像左边这幅图一样。
希帕索斯发现√2既不是整数也不是整数之比, 破坏了“万物皆数”这个信条,相传被毕达哥拉斯学派的人投入海中。
事实上, 根号2是一个无理数,就是不能表示成“整数之比”的数(我们在 讲 π 的时候讲过无理数的定义),是无限不循环的: √2=1.414213562…
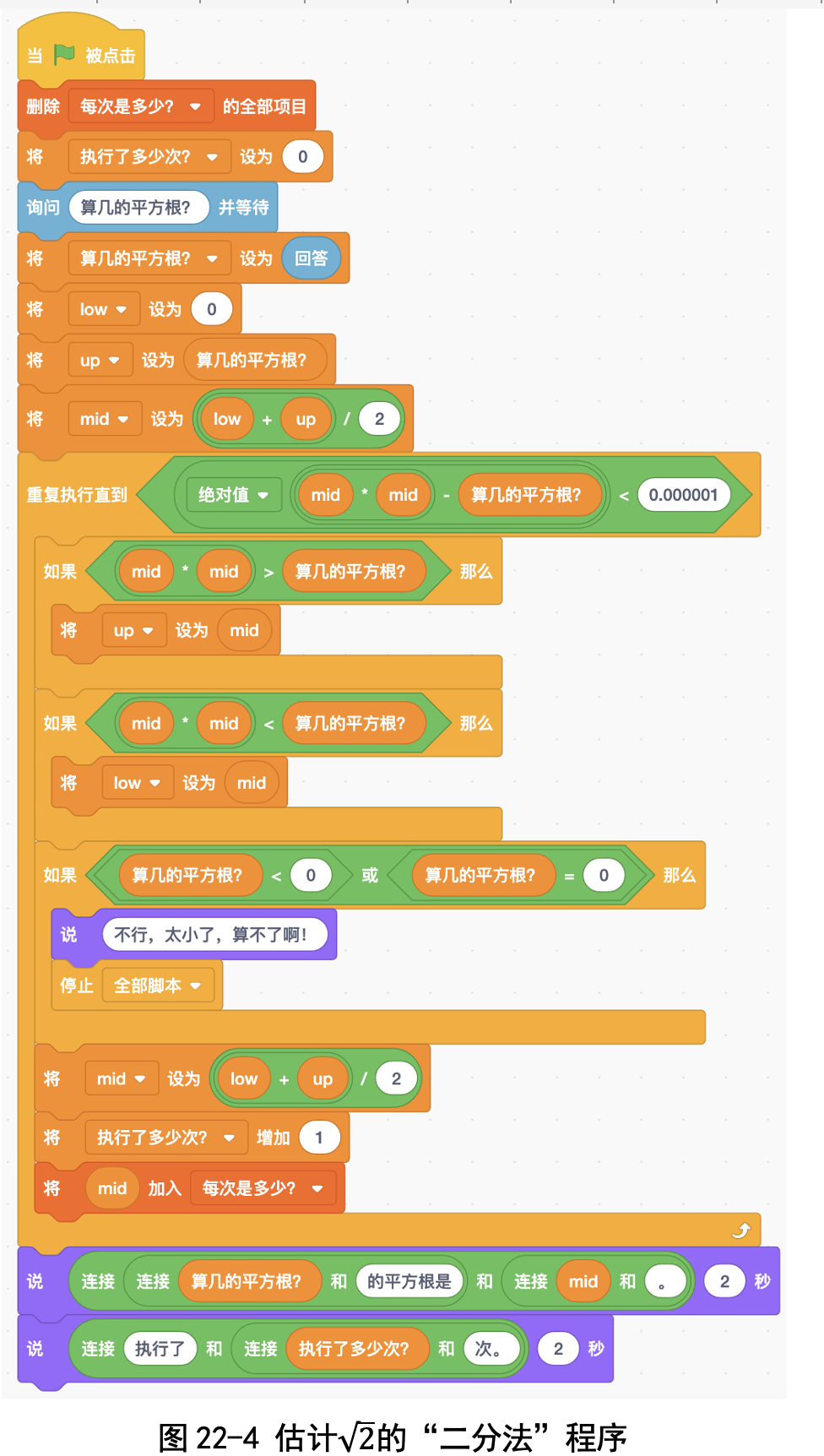
三、基本思路
刚刚我们用圆规把对角线转过来,发现对角线长度(也就是根号2)比 1 大, 比 2 小。包老师教我们把这个范围用中括号来表示,写成 [1, 2]。
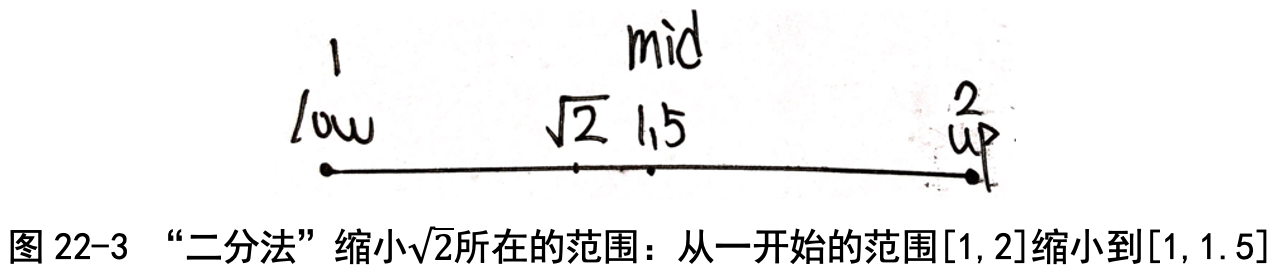
那能不能把这个范围缩小一点呢? 我们用上一讲学过的“二分法”缩小范围:1 和 2 之间的中点是 1.5,我 们先猜测√2=1.5。那这个猜测对不对呢?
包老师引导我们“反过来想”:“开根号我们不会,但是我们会平方啊。” 我们算一下 1.5 的平方:1.5×1.5 = 2.25,比 2 大,因此 1.5 肯定也比√2大。 因此, √2肯定在 [1,1.5] 这个范围之内。
你看,我们把根号2的可能范围缩小了一半了吧?我们这样不断重复,就能 把范围缩得越来越小,足够小之后就能精确估计出√2了。
代码下载及Web版
点击算平方根的代码下载于本地运行,或点击算平方根Web版直接运行
国内用户如果无法访问scratch.mit.edu的话,请点击国内可访问的Web版直接运行
点击算2的十二次方根的代码下载于本地运行,或点击算2的十二次方根Web版直接运行
国内用户如果无法访问scratch.mit.edu的话,请点击国内可访问的Web版直接运行
六、实验结果
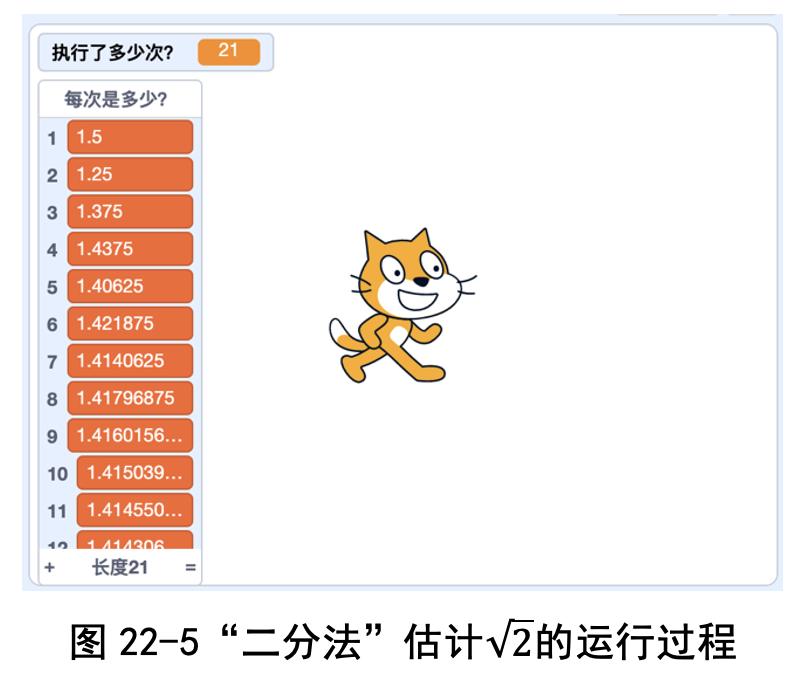
图 22-5 所示是程序的执行结果。我们能够看到一开始估计 √2=1.5,很 不准;第二次估计是 1.25,也不准;不过不要紧,再继续做,接下来是 1.375, 1.437, 1.406, 1.421,到第 10 次的时候,就估计出 √2=1.415,很接近 1.414 了。
### (一)除了 2,计算一下其他数的平方根,比如 3、5、7
### (二)输入不同的初始估计值 low 和 up,需要多少次循 环才能估计准?
这些内容请参见书中第22讲。
七、思考与延伸
(一)有没有更快的方法来估计出√2呢?
刚才我们每次都是取中间数 mid = (low + up)/2。难道一定要取中间点 吗?包老师说取这个范围中的任何一个数都可以,比如我们取得偏一点儿,用 黄金分割点:一开始的时候,我们估计在 [1, 2] 这个范围,也就是说 low = 1,up=2,下一次的估计值不取 1.5,而是取黄金分割点 1.618。
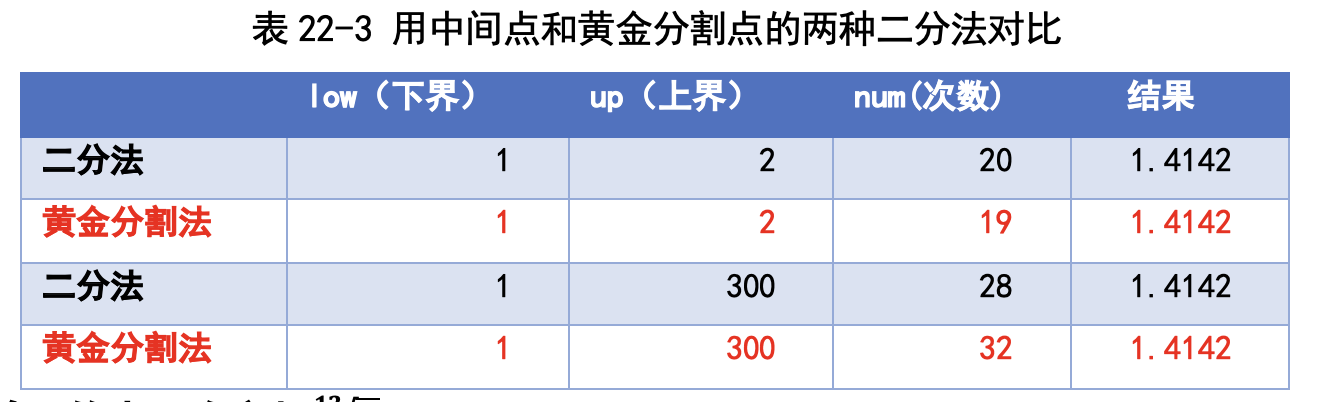
因为 1.618 的平方是 1.618×1.618 = 2.618,比 2 大,也就是说 1.618 肯定 比 √2大,所以我们可以断定 √2肯定在 [1, 1.618] 这个范围之内。这样就把范 围从 [1, 2] 缩小到 [1, 1.618],范围的大小变成了原来的 0.618。 我们发现:在上界比较大的时候,二分法比黄金分割法更快;在上界比较 小的时候,黄金分割法比二分法更快(见表 22-3)。
(二)计算 2 的十二次方根
咦?什么是2的十二次方根?其实类比一下,很好明白:2的平方根√2是这样一个数,它的平方(就是自己乘以自己)等于2。那2的十二次方根就是这样一个数,它的12次方(就是自己乘以自己,连乘12次)等于2。
2的十二次方根是啥我懂了,可是为啥要算它呢?
这背后有很好玩儿的故事。同学们大多数学过至少一件乐器的演奏,比如钢琴、小提琴等等。在学基础乐理的时候,音乐老师说过“八度”这个概念,就是钢琴上小字一组的C比中央C要高一个八度。那高一个八度到底是啥意思呢?我们打开钢琴的后盖就明白了,原来啊,对应小字一组C的那个琴弦比中央C的那根琴弦恰好短了1/2,反过来说,中央C的那根琴弦长度是小字一组C的2倍(图22-6)。
老师还教过我们一个概念,叫作“半音”:一个八度有12个半音;或者换句话说,从中央C到小字一组的C,有12个键(包括7个白键、5个黑键),相邻的键之间差1个半音。
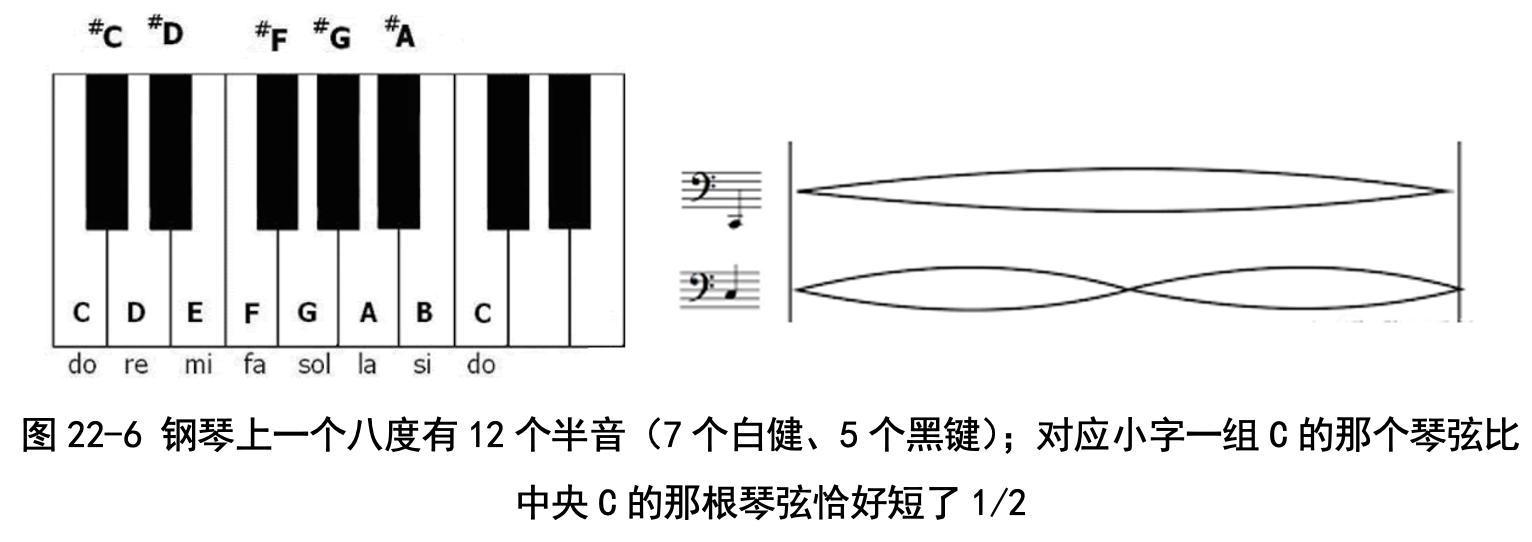
那问题来了:中央C的那根琴弦长度是小字一组C的2倍;中央C到小字一组C之间有12个键(就是12根琴弦),那相邻的琴弦之间长度之比是多少呢?
对啦!如果我们把相邻琴弦之间的长度之比设计成2的十二次方根的话,连乘12次,就得到2,那中央C的那根琴弦长度就正好是小字一组C的2倍啦。这种分法,能够分得非常均匀,叫作十二平均律;钢琴就是根据十二平均律定音的。
最后一个问题是:2的十二次方根到底是多少呢?是1.1?还是1.01?我们写个程序算一算吧!
我们已经学会了写程序算2的平方根等于多少,关键点是“反过来想”:平方根不会算,咱们就反过来想,算估计值的平方。我们先估计一个值,比如1.5,然后算它的平方1.5×1.5=2.25,比2大,说明我们估计得太高了,需要再调低一点儿。
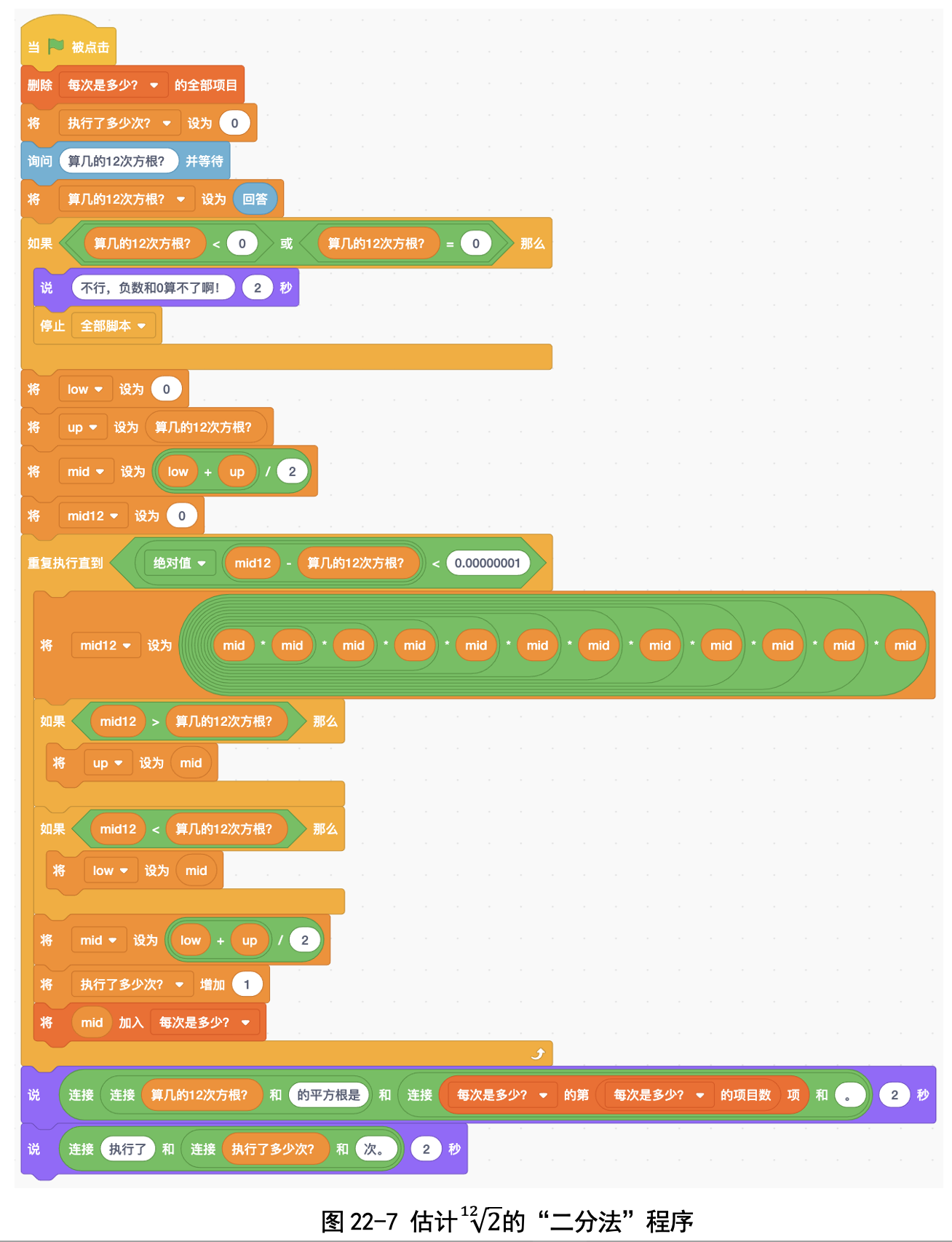
这里也一样,我们不会算2的十二次方根2的十二次方根,就反过来想,算估计值的12次方,然后跟2比大小,大的话就调低一点儿估计值,小的话就增加一点儿估计值。我们写的程序是这样的(图22-7)。
我们的程序估计出2的十二次方根=1.059463,精确到小数点后9位,非常准(图22-8)。
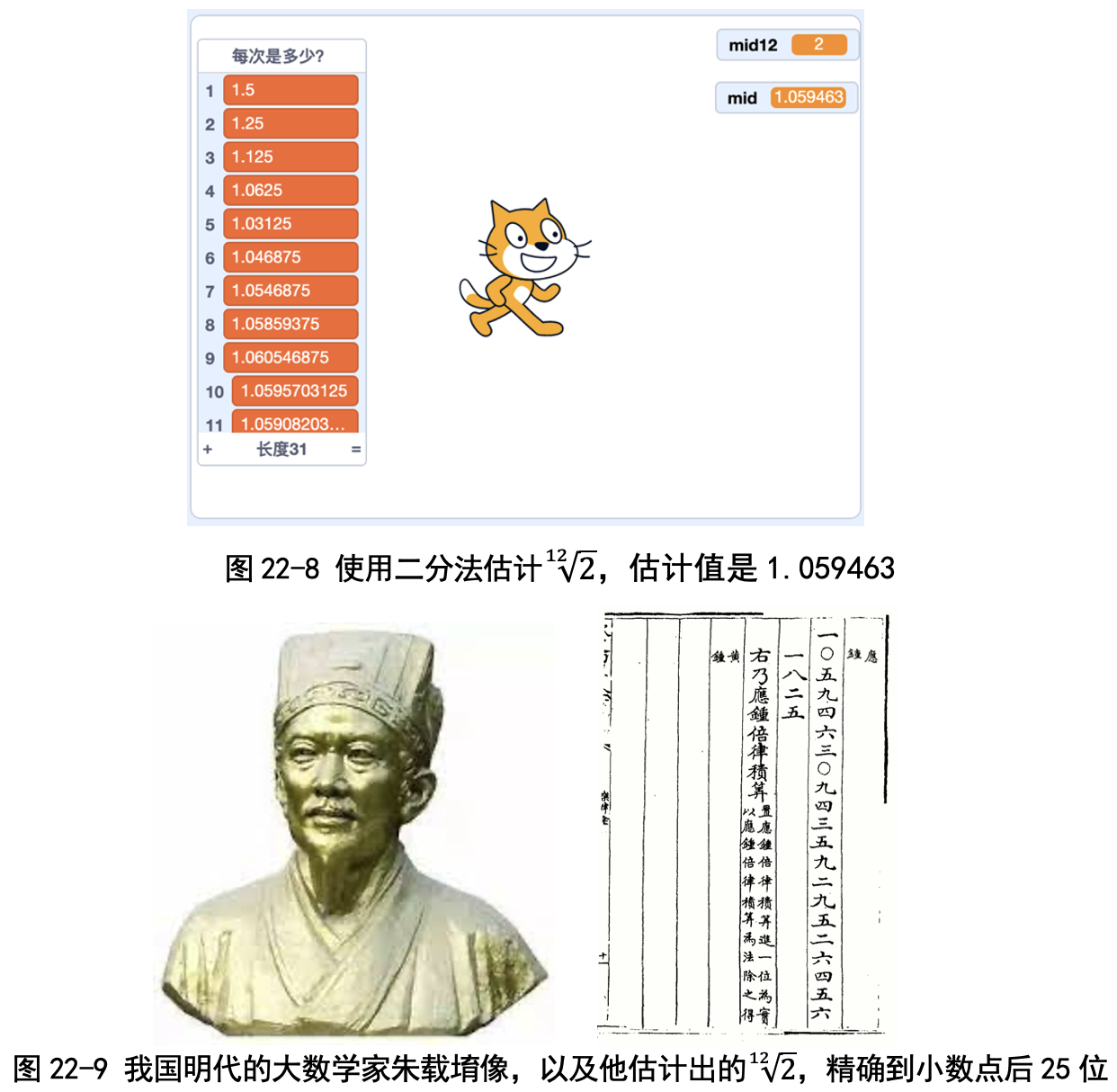
不过查了资料才知道,我国明朝时有位大数学家朱载堉,用算盘就算出来2的十二次方根=1.059463094359295264561825,达到了小数点后25位。太牛了!
卜老师告诉我们说:北大物理系武际可教授进行了考证,认为朱载堉算出来的2的十二次方根估计值通过传教士利玛窦传到了西方,促进了西方从羽管琴到现代钢琴的演变(要是不知道这个数的话,钢琴的琴弦该截多长呢?);物理学家亥姆霍兹也给予朱载堉极高的评价和赞誉(图22-9)。
八、教师点评
√2是历史上发现的第一个无理数。孩子们自己算出而不是简单背诵√2=1.414,有助于理解这个无理数。
开根号怎么算?孩子们一开始是手足无措的:只学过加减乘除,不知道怎样用加减乘除得到平方根。
这堂课最重要的东西就是“反过来想”:算平方根不会算,就转化成会算的平方。我们先估计一个值,比如1.5,然后算估计值1.5的平方:1.5×1.5=2.25,比2大,那1.5肯定也比√2大;我们就把估计值1.5调低一点儿,√2肯定在[1,1.5]这个范围之内。
一开始范围比较大,那不要紧;上堂课我们学过了“试错法”,就是不断地猜测、验证、修正,逐渐把范围缩小。
这种“反过来想”的思考方式,是我们希望孩子们能够记在心里的东西。
计算2的十二次方根背后的历史也值得一提:朱载堉没有电子计算器,只能用简陋的算盘,还是自制的“八十一档”大算盘;没有方便的阿拉伯数字“1, 2, 3, 4, 5, 6, 7, 8 , 9, 0”,只能有用汉字“一、二、三、四、五、六、七、八、九、〇”,却能完成这么精确的计算;其毅力之大、方法之妙,着实让人钦佩。