第 21 讲 玩游戏体会“二分法”:找钻石
一、实验目的
我们喜欢玩“数字炸弹”游戏。这个游戏是两个人(比方说小明和小红) 玩,规则是这样的:
小明想好一个 1~100 之间的数 x,但不把 x 说出来,让小红猜;小红可以 向小明提“Yes/No 型”的问题,小明诚实地回答 Yes 或者 No。考验小红的是: 如何用尽量少的提问,就把这个数 x 猜出来。举个例子,小明想好了数 x = 27。
● 小红问:x>50? 小明答:No。
● 小红问:x>25? 小明答:Yes。
● 小红问:x<38? 小明答:Yes。
● 小红问:x>32? 小明答:No。
● 小红问:x>28? 小明答:No。
● 小红问:x=27? 小明答:Yes!
小红用了 6 次提问,才猜出来小明想的这个数 x=27。
那小红选择哪些数提问,能够最快地找到答案呢?卜老师说最好的提问方 式是进行“二分法”提问,这样提问的好处是,无论答案是 Yes 还是 No,都 能够把候选数的范围缩小至少二分之一。这样的话,很快就能把范围缩小到只 有一个数,就是答案了!
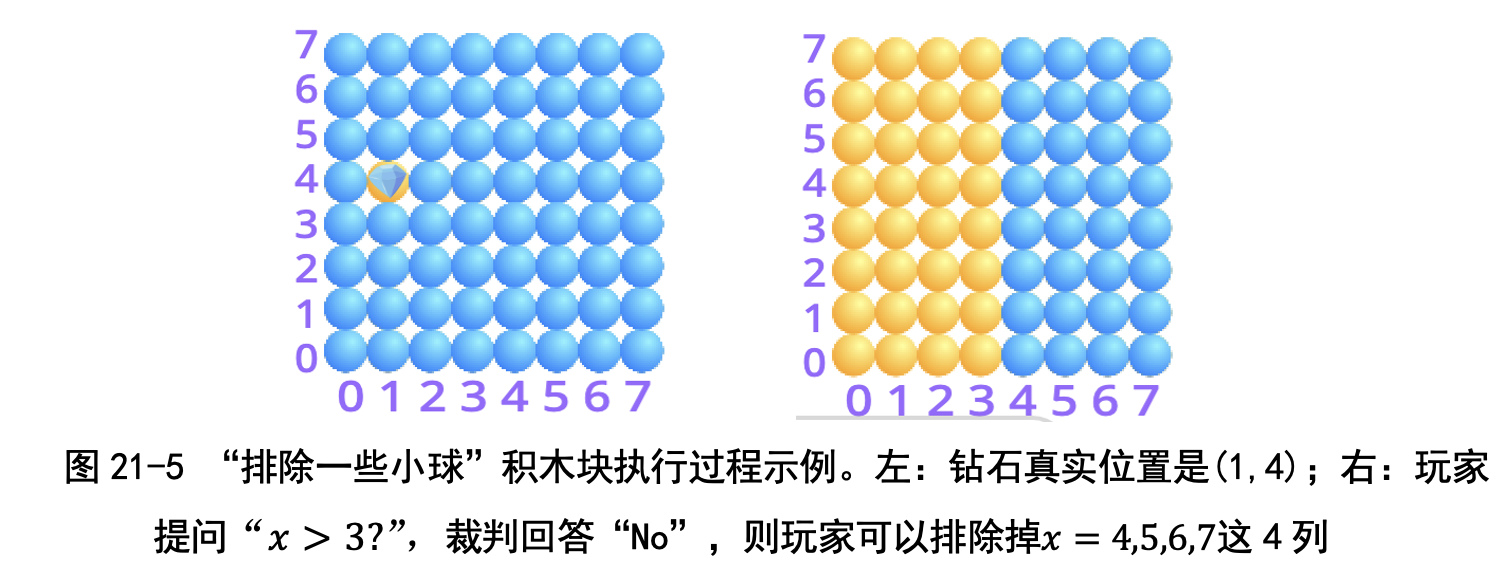
为了帮助我们理解二分法,卜老师设计了一个“找钻石”的小游戏:我们 有 8 行 8 列共 64 个小球,其中一个小球下面有一颗钻石,钻石的位置(x, y) 只有裁判员知道,我们不知道(见图 21-1)。
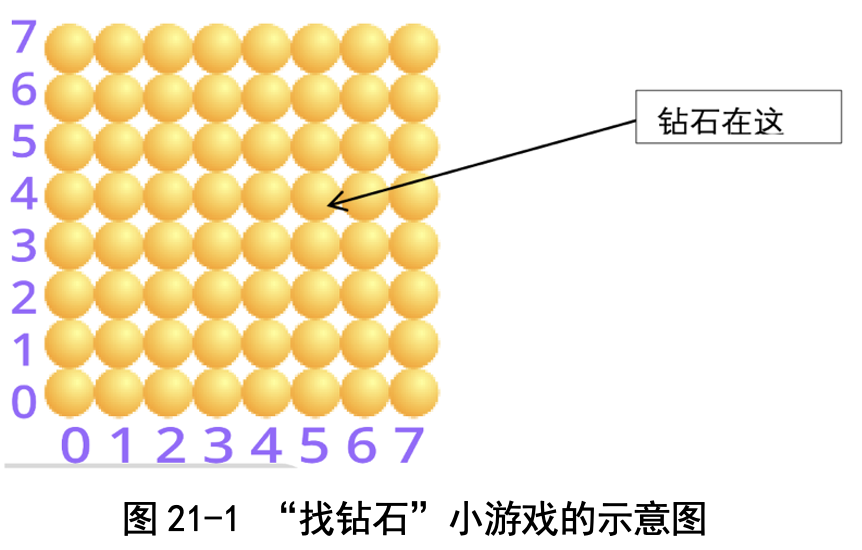
我们可以问两种类型的问题:
● 问钻石的 x 坐标:比如 x>3、x<5、x=2 ?
● 问钻石的 y 坐标:比如 y=5、y<3、y>4 ?
裁判诚实地回答 Yes 或者 No。我们的目的是问尽量少的问题来找到 钻石。
我们一起写程序吧!
二、背景知识
为了认识二分法的好处,我们先来看最简单的问法,也就是“逐个枚举” 了:先问x=0?x=1?…, x=7?再问y=0? y=1?…, y=7?这样最多问16个问 题肯定能找到钻石。不过这个方法问的问题有点太多了。我们可以用一个聪明 的方法,就是“二分法”。
二分法的优势在于每次可以消除一半的可能性。比如先问 x>3 ?
● 如果裁判回答 Yes,那么我们就可以不再考虑 x=0, 1, 2, 3 这些位置,这 样 x 的候选范围就只剩下一半的数量了。
● 如果裁判回答 No,那么我们就可以把 x = 4, 5, 6, 7 这些位置去掉,这样 x 的候选范围也是只剩下一半的数量了。
每次都这样用二分法去做,每次把候选范围缩小一半,只用很少的提问就 可以了。
三、基本思路
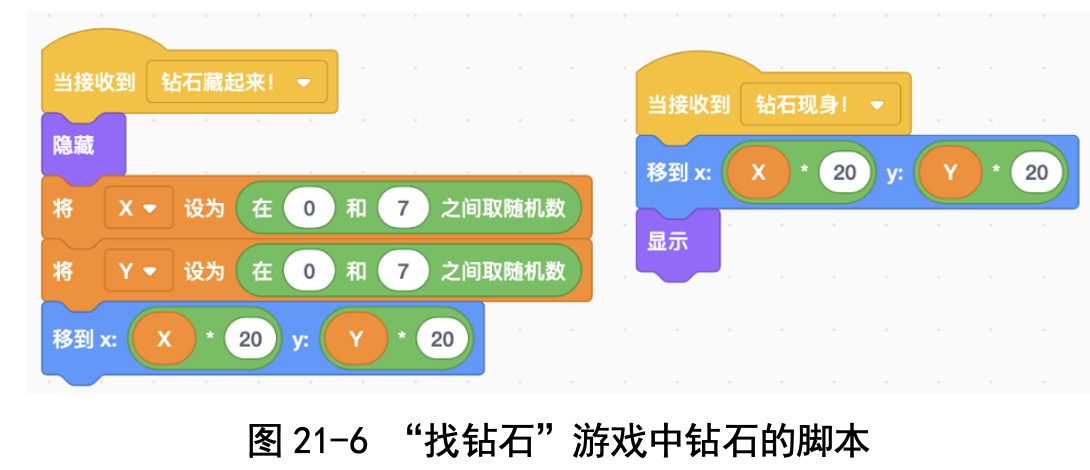
玩家在输入提问之后,裁判员将不满足条件的小球改变颜色,然后游戏者 继续输入提问,裁判员再将不满足条件的小球改变颜色。如此重复,直到找到 钻石为止。
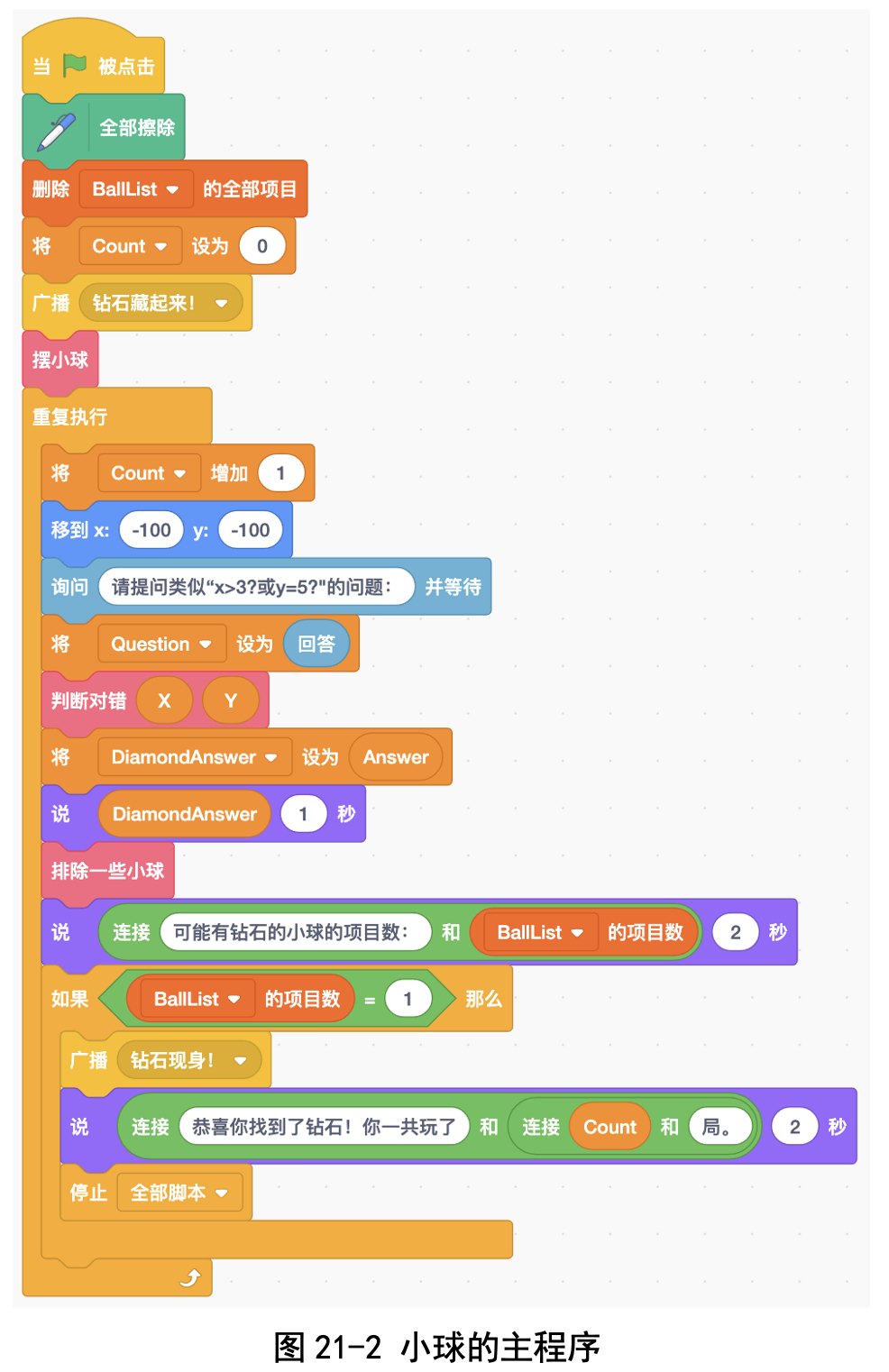
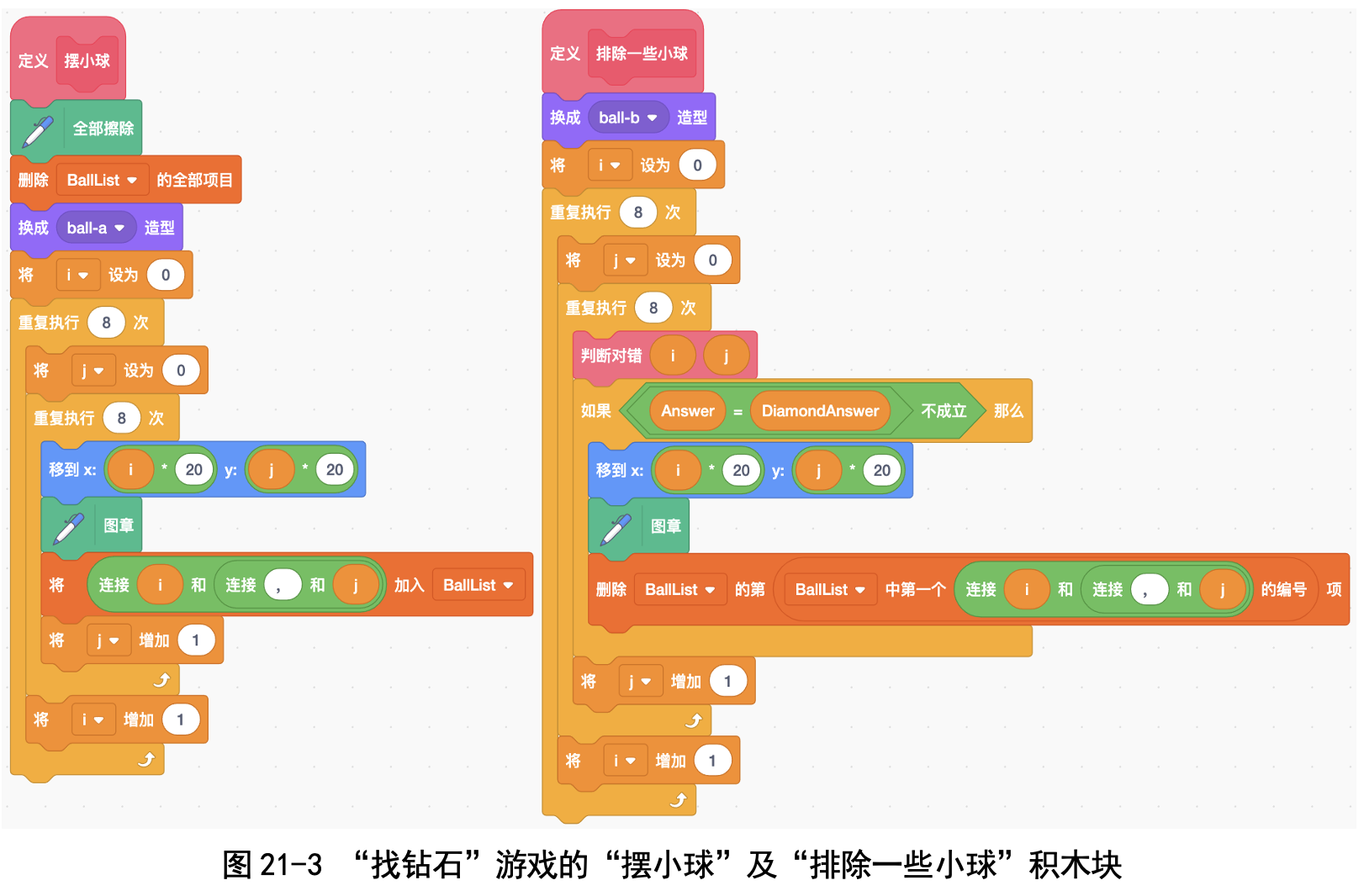
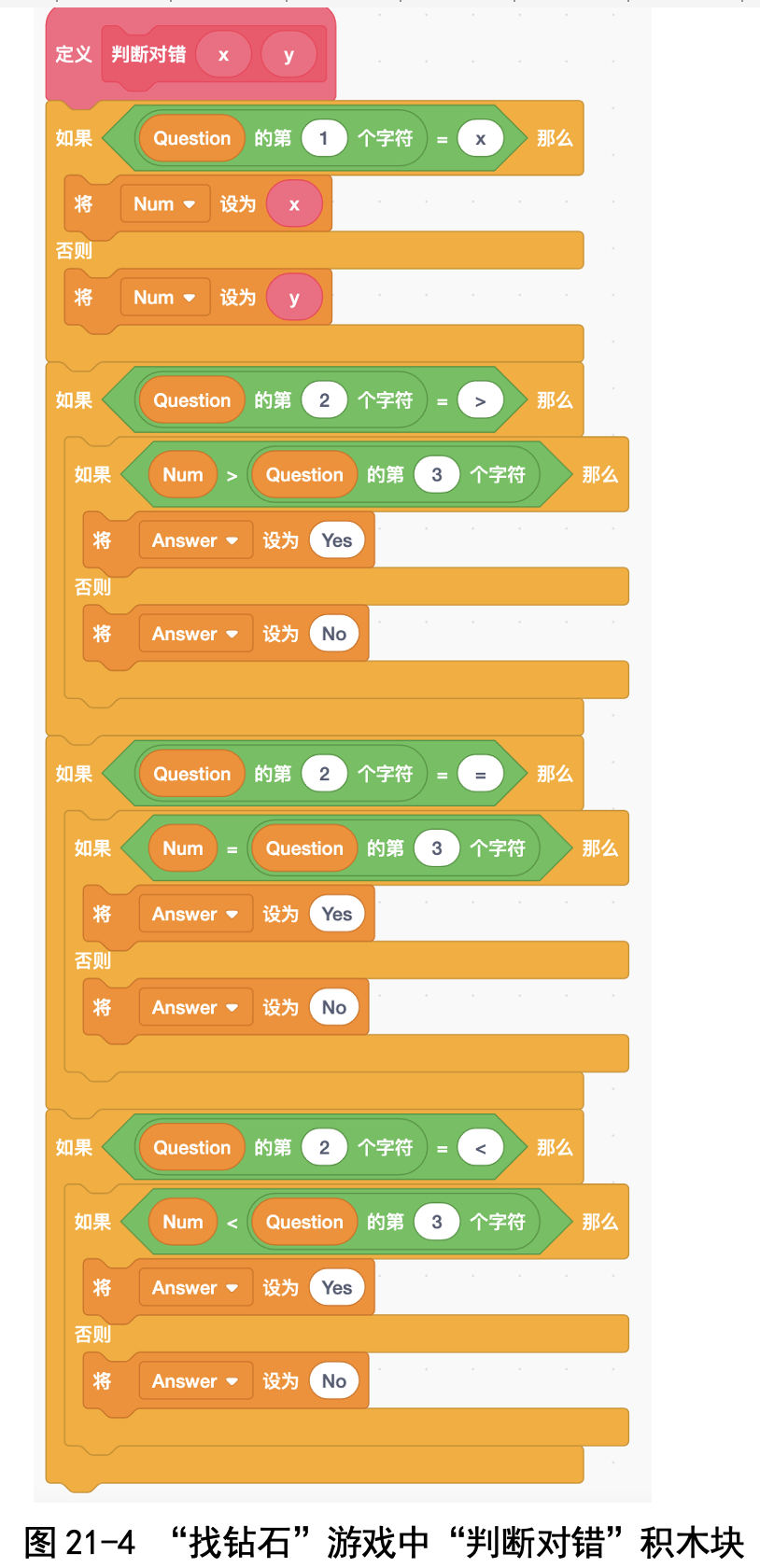
代码下载及Web版
点击找钻石游戏的代码(发送消息版)下载于本地运行,或点击找钻石游戏Web版(发送消息版)直接运行
国内用户如果无法访问scratch.mit.edu的话,请点击国内可访问的Web版直接运行
找钻石游戏的代码(简洁版)下载于本地运行,或点击找钻石游戏Web版(简洁版)直接运行
国内用户如果无法访问scratch.mit.edu的话,请点击国内可访问的Web版直接运行
六、实验结果及分析
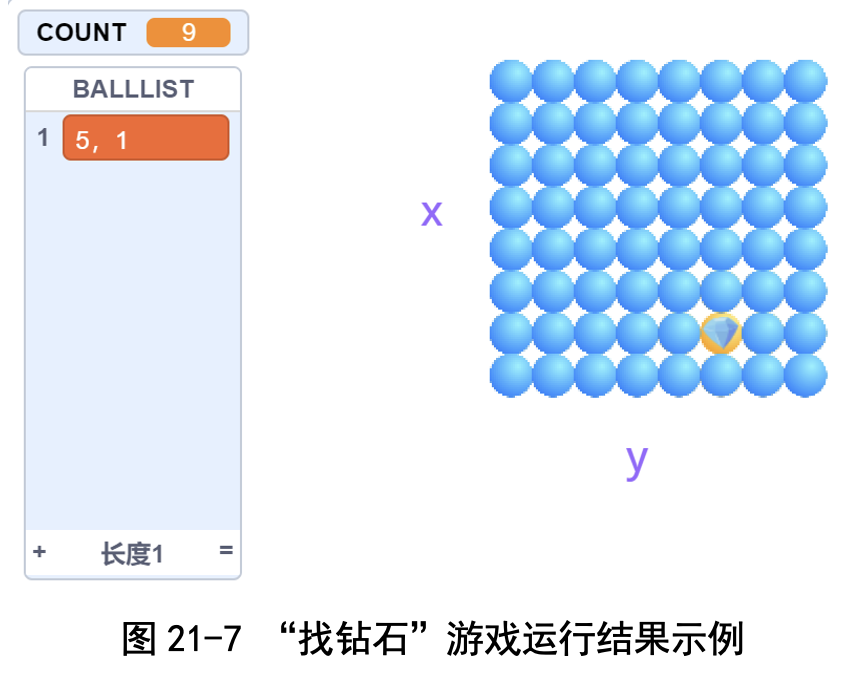
我玩第一局时,用了 9 次提问(见图 21-7)。玩第二局时,只用了 5 次提 问就可以了。第二次比第一次快,是因为第二次用了二分法,而第一次没有用 二分法。
七、思考与延伸
(一)采用什么样的策略最合适?
采用二分法最好,因为每次都可以排除至少一半的小球。
(二)傅鼎荃说对 8 行 8 列的游戏来说,使用二分法最多 需要 6 次,为什么?
因为用二分法可以排除一半所以就是 64÷2÷2…,不断除以 2,直到得到 1。我发现有 6 个除号就能把 64 变成 1,所以最多只需要 6 次啦!
刚才我们是从除法的角度计算,如果从乘法的角度来看,我们问的实际上 是“2的几次方等于64”,用对数表示就是$\log_2 64=?$
什么叫对数呢? 比如2的3 次方等于 8,我们就说 8 的对数是 3 ;2 的 6 次方等于 64,我们就说 64 的对 数是 6。
(三)用递归的观点想一想
我是这样理解递归的:在两面相对的镜子之间放一根正在燃烧的蜡烛,我 们会从其中一面镜子里看到一根蜡烛,蜡烛后面又有一面镜子,镜子里面又 有一根蜡烛……这就是递归。在这一讲中,64÷2÷2…中的不断除以 2 也是 递归。
八、教师点评
“数字炸弹”是一个很好的游戏,孩子们在玩这个游戏时,能够自然而然 地领会到“二分法”。二分法的好处是:无论猜对还是猜错,都至少能够排除 掉 1/2 的选项。
这个游戏的另一个用意就是引导孩子们领会“猜测 - 修正”解题策略。在 解决问题时,我们一定要勇敢地去尝试、去猜测,猜错了不要紧,想办法修正 就是了。