第 20 讲 玩游戏体会“搜索法”:走迷宫
一、实验目的
卜老师教我们解数学题的时候一再强调:解题就是搜索,就是找路,找出 一条从“已知条件”到“待求的目标”的路。
找路就得从当前已推出的结果选择一个方向走走试试,要探索,要尝试; 走得通就走,走不通就退回来重新选择一个方向继续尝试。关键是要积极尝 试,还要善于尝试,也就是选择好尝试的方向。
这跟我们走迷宫非常像,圆明园里有一个用一人高的砖墙建造的迷宫“万 花阵”(见图 20-1 中左侧部分),迷宫里的道路上有很多分叉口,还有些路是死 胡同。从入口进去之后,想要到达出口可不容易。我是在不知所措的时候,让 爸爸把我举起来看路才走出来的。

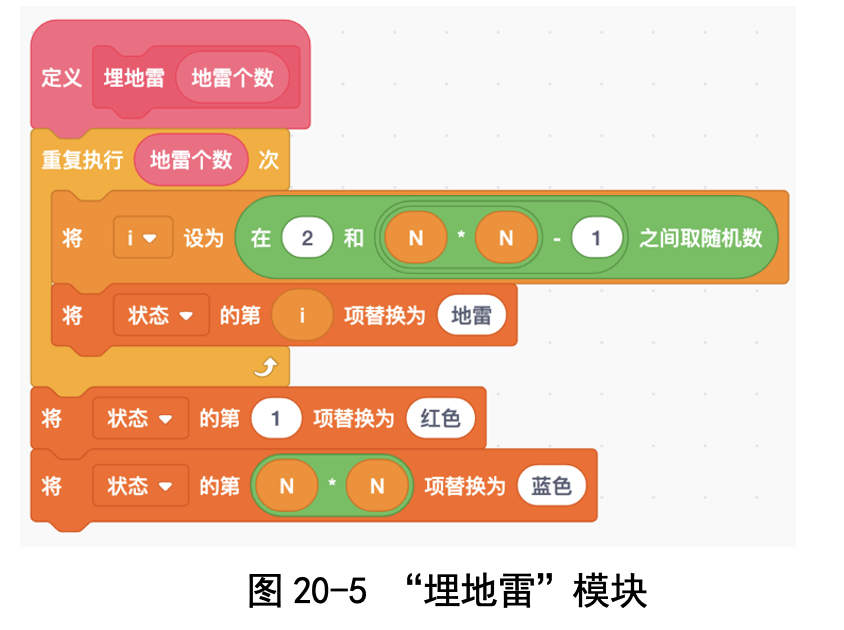
为了加深我们对解题策略的理解,卜老师设计了一个“走迷宫”的小游戏: 我们用 7 行 7 列的小球表示迷宫,有入口,有出口,中间有些地方埋有地雷, 表示此路不通(见图 20-1 中右侧部分)。当然了,地雷埋在哪里事先是不知道 的,只有踩到了才知道。问:怎样从入口尽快地走到出口?
走这个迷宫的规则是:
● 每次只能从与当前位置相邻的点选择一个。
● 也可以从出口往回试探。
● 有些地方埋有地雷,表示此路不通,得退回去重新选择。
我们来实现这个小游戏吧!
二、基本思路
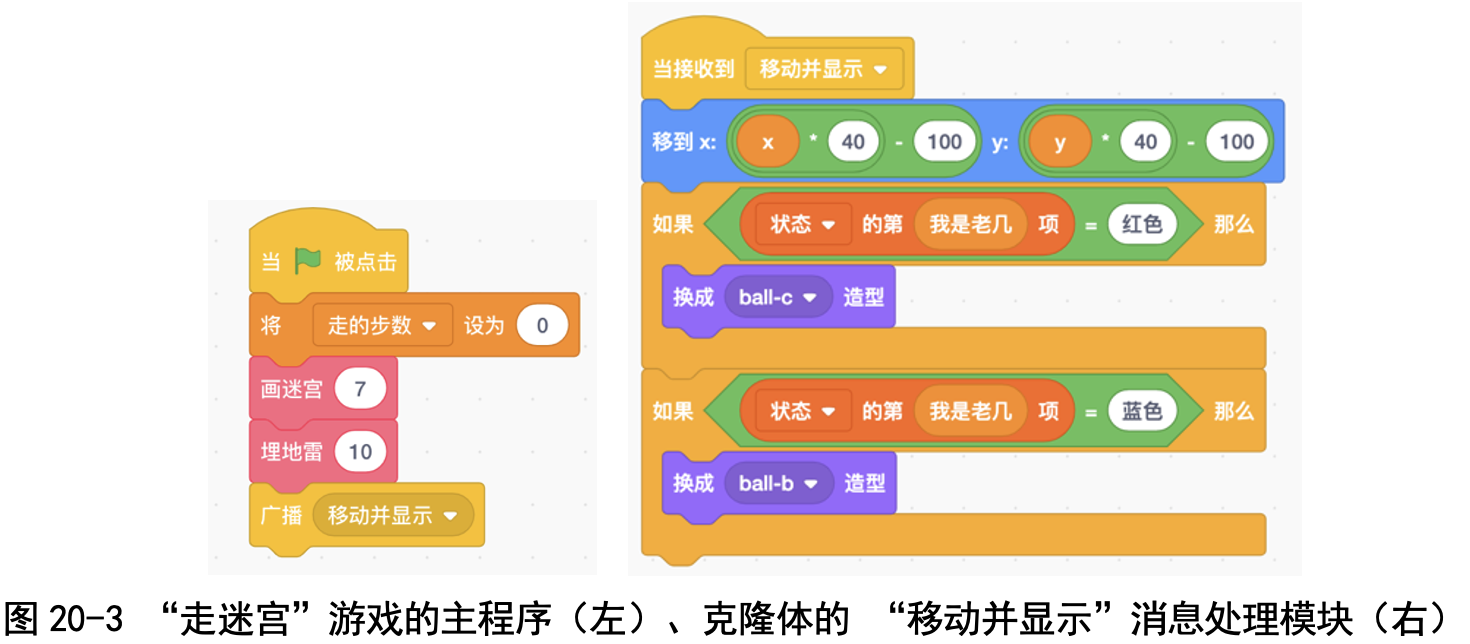
我们总共有 7×7 = 49 个小球,要是为每个小球都创建一个角色的话,那 还得为每个小球都写一段脚本,就太麻烦了!
一个高效的实现方法是应用“克隆”技术:因为所有小球的脚本都是一样 的,所以我们可以建立小球的 49 个克隆体,这样只要写一份脚本就可以了, 方便吧?
我们给小球染上颜色,表示如下意思:
● 红色:表示能够从“入口到达此处”,换句话说,我们已经“找到过从 入口到达这里的一条路”。
● 蓝色:表示能够从“此处到达出口”,换句话说,我们已经“找到过从 出口到达这里的一条路”。
● 黄色:表示还不知道怎样从入口到达这里,也不知道如何从出口到达 这里。
一开始的时候,左下角入口处的小球克隆体是红色的,右上角出口处的小 球克隆体是蓝色的,其他小球都是黄色的。每当点击一个小球时,这个小球会 收到“角色被点击”的消息,它就做如下检查和判断:
● 如果小球下面埋着地雷,则隐身,表示“此路不通”。
● 如果上下左右的邻居中同时有红色和蓝色,则意味着“找到了一条从入 口到出口的通路”,成功结束。
● 如果邻居中有红色的,则从这个邻居可以到达小球所在位置,因为从入 口可以到达这个邻居(邻居是红色的),所以可以从入口经过这个邻居 到达这个小球处,我们就把这个小球也设置成“红色”。
● 如果邻居中有蓝色的,则从这个邻居可以到达小球所在位置,因为从出 口可以到达这个邻居(邻居是蓝色的),所以可以从出口经过这个邻居 到达这个小球处,我们就把这个小球也设置成“蓝色”。
● 如果邻居中既没有红色的,也没有蓝色的,则表示我们还不知道怎样从 入口到达这里,也不知道如何从出口到达这里,小球保持原有的黄色。



代码下载及Web版
点击走迷宫的代码下载于本地运行,或点击走迷宫Web版直接运行
国内用户如果无法访问scratch.mit.edu的话,请点击国内可访问的Web版直接运行
五、实验结果及分析
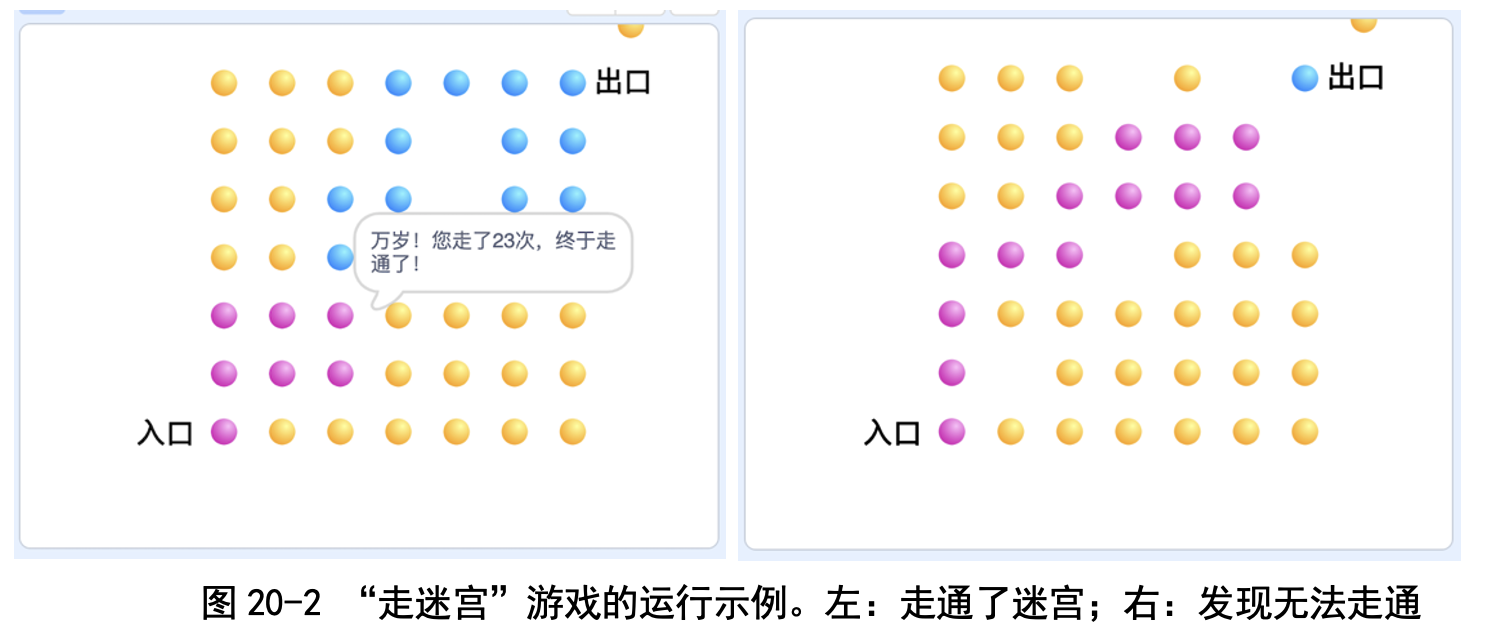
这个游戏很好玩:走的时候战战兢兢,不知道脚下是否有地雷,还有就是 发现走不通之后,得琢磨退回哪个点再重新开始(见图 20-2)。
我往往是从入口开始试,再从出口倒着走试试,有时能够成功走通!在我 看来,大家刚开始玩的时候,要把地雷的数量设少一点,要不然经常会出现无 路可走的情况哦!
六、思考与延伸
(一)采用什么样的策略走最合适?
我觉得从入口走的时候“一上一右”尝试最合适,从出口倒着走的时候 “一下一左”尝试最合适。这样做的好处是不会太偏离目标。
(二)“走迷宫”和解数学题之间有什么关系?
在解数学题时,已知条件是入口,求解目标是出口;每次求解就是从入 口向前试探着走一步,或者从出口往回走一步。如果走通了,就表示求解成 功了。
我们学数学的时候,尝试过好几次这种解题策略,很有效果,解题的时候 不会毫无头绪了,也不会在纸上写得丢三落四,漏掉重要的中间结果了。
好了,最后祝大家玩得愉快!
七、教师点评
“走迷宫”游戏能够很好地锻炼孩子们的思维方式:在只知道整体目标的 情况下,当前碰到分叉口怎么选择?如果走着走着走到死胡同了,该退回到哪 里重新走呢?
很多事情本质上就是“走迷宫”。比如解数学题,已知条件就是迷宫入口, 要证明或求解的目标是迷宫出口,每一步都可沿着多个方向尝试推导,每一个 方向就是一个分叉,推着推着,推不下去了,或者偏离目标太远了,就得赶紧 想着退回到哪里再继续尝试。哪条路能够走通,哪条路有坑,是无法预知的。
陶哲轩写过一本小册子《跟陶哲轩学解题》,说分享了他的解题方法:拿 一张大纸,顶上写已知条件,底下写待求解的目标,然后从已知条件向下推 理,推出的中间结论都先记录下来,直到能够推导出目标。当然了,不仅可以从已知条件向下推理,还可以从目标倒推,就是明确“要证明目标成立,需要 有哪些条件”,只要最后找到一条“从已知到目标”的路就成功了。
除了解数学题之外,科学研究的过程也是“走迷宫”,也是不断地尝试、 摸索、回溯,时刻衡量当前距离整体目标还有多远、是否偏离目标,有时甚至 连整体目标都不能事先定义清楚,是一种朦胧的状态。
我们设计这个游戏的初衷,就是希望孩子们在玩这个游戏的过程中体会到 搜索、回溯,选择尝试的策略,判断是否偏离目标,并在将来解数学题、做研 究时能够自然而然地应用起来。
至于这个游戏的程序设计部分,用到了克隆、私有变量的定义、列表等, 是对孩子们编程能力的综合检验。