第 15 讲 用“试错法”求解鸡兔同笼问题
一、实验目的
今天我们编程求解鸡兔同笼问题,就是请用户输入鸡和兔子的总头数和总 腿数,程序要输出鸡的数目和兔子的数目。
二、背景知识
(一)什么是鸡兔同笼问题?
鸡兔同笼是我国古代著名趣题之一。大约在公元四、五世纪,《孙子算经》 中就记载了这个有趣的问题,书中是这样叙述的:“今有雉、兔同笼,上有 三十五头,下有九十四足,问雉、兔各几何?”这里的“雉”就是鸡的意思。
这段话的意思就是鸡与兔子混在同一笼内,已知鸡兔共有的只数与腿数, 求有几只兔子几只鸡(见图 15-1)。
(二)怎样求解鸡兔同笼问题?
(1)试错法
试错法是一种重要的思考问题的方法,包括“尝试,验证对错,如果错误 则修正后继续尝试”三步。
详细地说,我们先假设待求的数取某一个值,然后 通过推导、验证已知条件,看这个假设对不对;如果不对,则想办法修正这个 假设。这样不断修正,最后求出问题的解来。
用试错法解答鸡兔同笼问题就可以先假设笼子里全是鸡,于是根据鸡兔的 总数就可以算出共有几条腿,把这样得到的腿数与题中给出的总腿数相比较, 如果一致则求解完毕,否则看看差多少条腿,每差 2 条腿就说明有 1 只兔子, 因此将所差的腿数除以 2,就可以算出共有多少只兔子。
以《孙子算经》记载的问题为例,用假设法求解的过程如下:
假设笼子里全是鸡,即鸡有 35 只,兔子有 0 只,则一共有 35×2=70 条 腿,但是已知总腿数是 94,这比总腿数少 24 条。
看来全都是鸡这个假设不 对,那该怎样修正假设呢?我们尝试修正一下:
● 要是少 1 只鸡的话,即有 34 只鸡和 1 只兔子的话,共有 34×2+1×4=72 条腿;
● 要是少 2 只鸡的话,即有 33 只鸡和 2 只兔子的话,共有 33×2+2×4=74 条腿。
这时候几位同学都看出规律来了:每少 1 只鸡,就多 1 只兔子,会多出 2 条腿。刚刚我们已经看到,当假设全部都是鸡的时候,少了 24 条腿;因此, 应该有 24÷2=12 只兔子,有 35-12=23 只鸡。
(2)列方程法
列方程解题有个小窍门:凡是不知道的数(叫未知数),先用一个符号表 示,比如 x, y, z 等,然后把已知条件用这些未知数表示成等式。先把方程列出 来,再看怎样解这些方程,求出未知数。
在“鸡兔同笼”的问题中,可以设有 x 只兔子,然后根据鸡、兔的只数与 腿数的关系列出方程来。以上面的问题为例,用列方程法求解:
设有 x 只兔子,则鸡有 35-x 只,总腿数是 4×x+2×(35-x)。现在我们又 已知总腿数是 94,因此可以列出等式:
4×x+2×(35-x)=94
化简一下,可以得到: 2×x+2×35=94
最终可以得出 x=12,即兔子有 12 只,鸡有 23 只。
三、基本思路
我们采用“试错法”来编程求解鸡兔同笼问题:我们尝试猜测鸡的数目。 详细地说,先尝试鸡的数目是 0,逐渐增加到总头数;对每一次尝试,都算出 兔子的数目,再算出总腿数,并和已知的总腿数比较,看两者是否一致,如果 一致,则找到了答案,否则就增加鸡的数目。
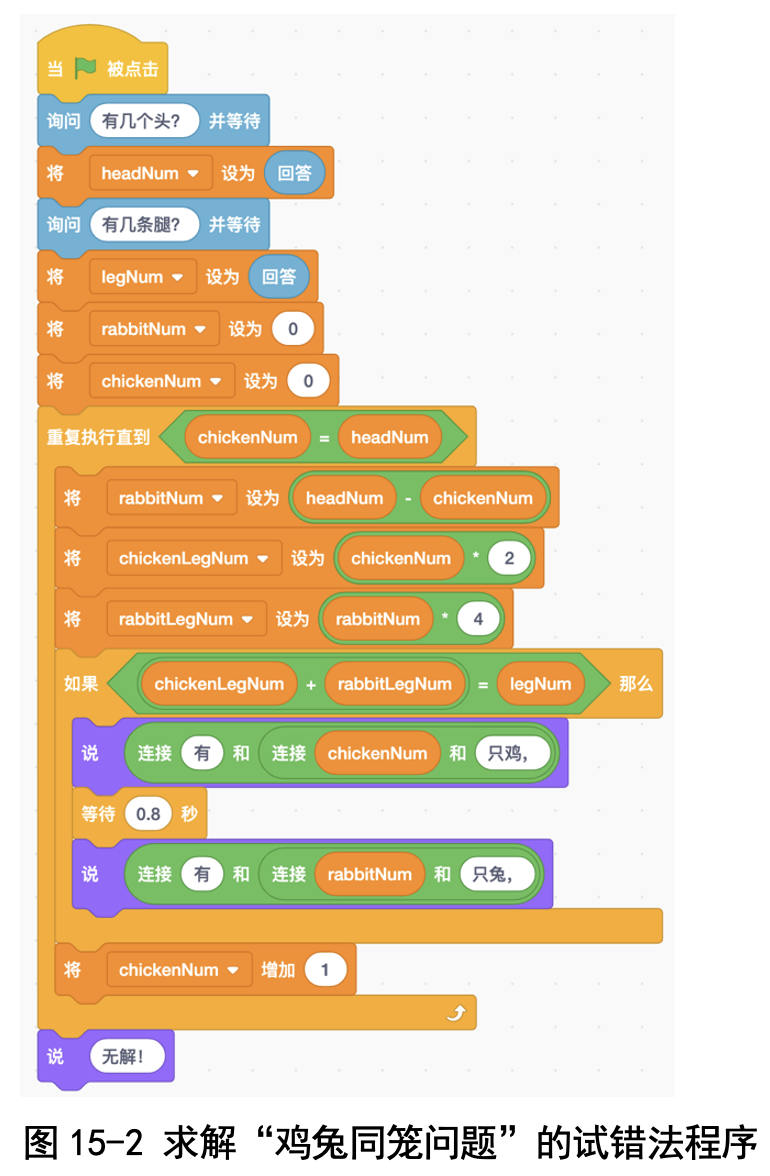
这里的“尝试 - 验证 - 再尝试”循环就用“重复执行直到”积木块实现吧!
代码下载及Web版
点击求解鸡兔同笼问题的代码下载于本地运行,或点击鸡兔同笼Web版直接运行
国内用户如果无法访问scratch.mit.edu的话,请点击国内可访问的Web版直接运行
六、实验结果
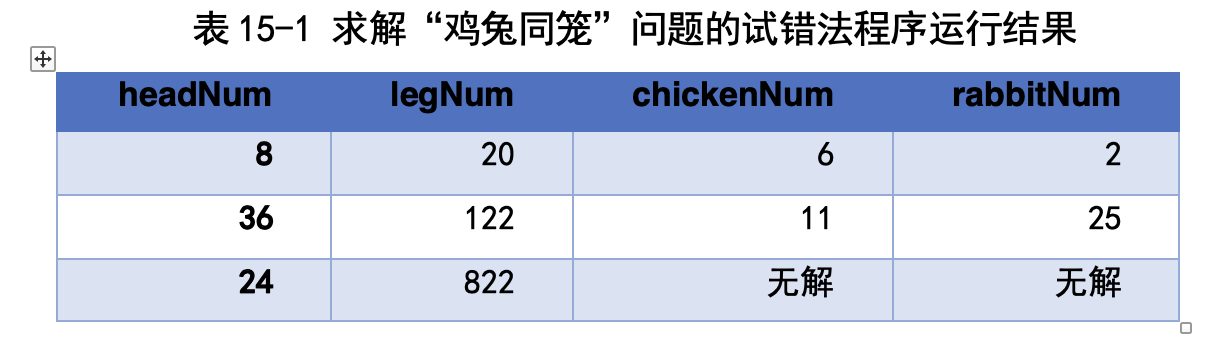
输入几组不同的 headNum 和 legNum,程序的输出如表 15-1 所示。前两 组都是对的;最后一组有 24 个头,但是却有 822 条腿,这显然不可能,程序 报告“无解”。
七、思考与延伸
(1)鸡兔同笼问题中腿的总数量能否为奇数?
(2)用鸡兔同笼问题的解法可解决类似的问题:停车场上共停放 56 辆小 轿车和自行车,两种车轮子数总和为 38 个,小轿车和自行车各有几辆?
(3)把上面的问题中的自行车换成三轮车呢?
八、教师点评
鸡兔同笼是经典问题。我在给孩子们上数学课时讲过这个问题,当时引导 孩子们用“试错法”思考。试错法是一种“正向”的思维方式,首先能够促进 孩子们理解题意,更重要的是能够促进孩子们去大胆尝试。 与之相反,求解问题是一个“逆向”思考过程,只有在进行充分的正向思 考、弄懂问题的意思之后,才能更好地理解逆向解法,甚至自己发现逆向解 法。从教学的角度来说,直接教“逆向”求解法也不是不可以,但是往往会有 一些害处:孩子们只是单纯地背会了解法,对于这种解法是怎样得出来的,自 己能否想出来却没有头绪。
在引导孩子们采用“正向”思维方式进行尝试时,还发生了一件令我吃惊 的事情:傅鼎荃同学自发地想出了“折半查找法”。当时我们求解《孙子算经》 里的例子,我在黑板上画出了这样的表格,表示尝试过程(见表 15-2)。
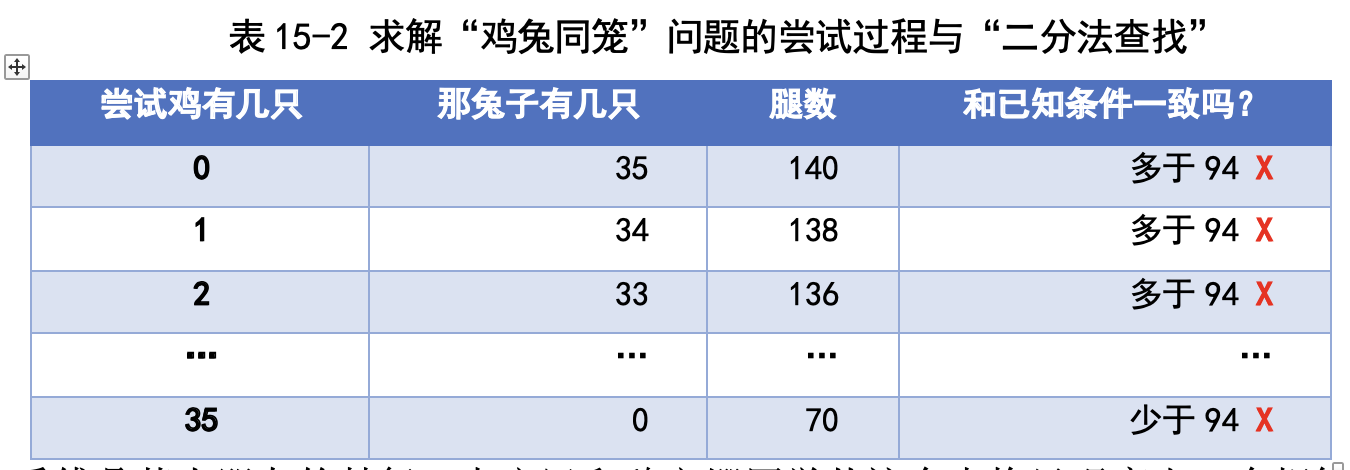
当我带着孩子们尝试到鸡有 2 只时,孩子们说:“这样算下去,太累了! 腿数总是远远多于 94 !老师,咱们干脆尝试鸡有 35 只试试看。”
于是我们就直接尝试鸡有 35 只是否正确;我在表格中间空了一行,表示 跳过了一些尝试。
结果很不幸,这次也不对,腿数又太少了!现在该尝试鸡有多少只,是 从大到小尝试鸡有 34 只,还是继续刚才的从小到大的过程,尝试一下鸡有 3 只呢?
这时傅鼎荃同学站起来说:“老师,咱们不尝试有 34 只鸡,也不尝试有 3 只鸡,而是从中间尝试,试试鸡有 17 只行不行”。这是计算机里经典的“折半 查找法”啊!我们从来没有教过孩子们这个方法,这完全是傅鼎荃自发地想出 了这个方法!这是我们“慢数学”教学的一个小小的胜利!
受傅鼎荃小朋友的鼓舞,卜文远和魏文姗同学从这个表格里观察出一个规 律:每多 1 只鸡,就少 2 条腿。这样不用枚举也行啊!至此,可以说孩子们已 经完全掌握了这个问题的求解方法。甚至后来碰到“铁块重 3 千克,铜块重 5 千克,已知共 6 块金属,总重量 20 千克”的问题时,也立刻反应出这就是鸡 兔同笼问题。
至于列方程求解法,孩子们反而觉得太麻烦:列方程简单,解方程好难。 我们干脆只要求孩子们会列方程即可,至于解方程,让孩子们用“方程求解” 软件 https://zh.numberempire.com/equationsolver.php 就行了,孩子们很高兴!