第13讲 再论聪明的枚举:三阶幻方
一、实验目的
三阶幻方是一个有趣的游戏。这个游戏是这么玩的:有一个 3 行 3 列的九 宫格,让我们把数字 1~9 填入格子之内,每个格子只 能填一个数,要求是每行、每列、每条对角线的加和都 相等。比如图 13-1 中就是一种填法。
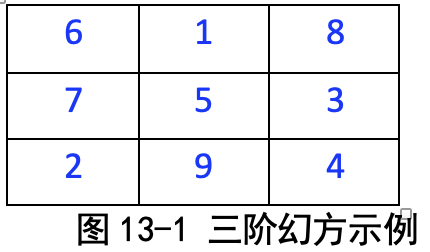
我们验算一下:
行和 6+1+8=7+5+3=2+9+4=15,
列和 6+7+2=1+5+9=8+3+ 4=15,
两条对角线 6+5+4=8+5+2=15,
的确都相等。
包老师问我们:“除了这种填法之外,还有多少种填法?能不能写个程序 把所有的填法都找出来呢?”
二、背景知识
(一)什么是幻方?
三阶幻方是最简单的幻方,是由 9 个数组成的一个 3 行 3 列的矩阵,其每 一行、每一列和两条对角线的数字之和(称为幻和值)都相等。
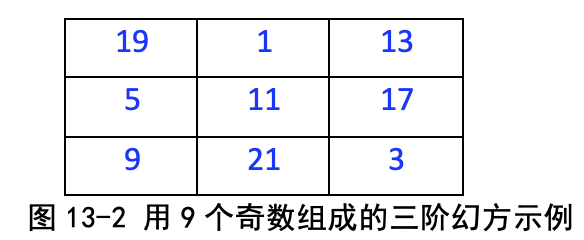
一般常常用 1, 2, 3, …, 9 这 9 个数填三阶幻方, 不过也可以换用其他数,比如,用 1, 3, 5, 9, 11, 13, 17, 19, 21 这 9 个奇数组成图 13-2 所示的三阶幻方。 你看这里的幻和值等于 33,和上一个幻方完全不一 样了。
(四)三阶幻方的“包卜魏猜想”
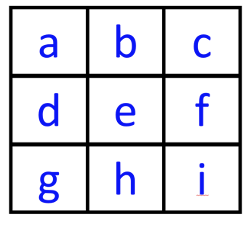
我们三个(包若宁、卜文远和魏文珊)发现了一个规律:只要知道 3 个数, 即中心数 e,左中数字 d,左上角数字 a,就能唯一确定三阶幻方!
我们的步骤是这样的:
(1)第一步:既然知道了 e,那么幻和值就能求出来了,肯定是 3e。
(2)第二步:知道了 a, d,用幻和值减去 a 和 d,就能得到 g。
(3)第三步:知道了 a, e,用幻和值减去 a 和 e,就能得到 i。
这样一步一步推导,就能把整个幻方全部推出来了!这种方法不仅适用于 由 1~9 组成的幻方,由其他数构成的幻方也适用!图 13-4 是我们当时在黑板 上推理时画的幻方。
发现了这个规律,我们太兴奋了!老师也非常高兴,把我们这种方法命名 为“包卜魏猜想”。我们也有以自己名字命名的猜想啦!

三、基本思路
(一)最笨的填法是怎么的?
我们可以枚举所有可能的填法,然后检验每种填法,判断是否构成幻方。 比如:如果将 a 设为 1,那么 b 就要从 2~9里选择一个数,有 8 种可能;如 果将 b 设为 2,那么 c 就要从 3~9 中选择一个数,有 7 种可能;因此,将 9 个数填入 3×3 的表格,一共有 9×8×7×6×5×4×3×2×1=360880 种可能 的排列,每种情况需要进行 8 次判断(检查 3 行之和、3 列之和、3 条对角线 之和),来判断是否构成三阶幻方。
(二)聪明的方法怎么填?
刚才那种枚举的组合太多了!老师在给我们讲“数字谜”问题的时候就一 再强调,枚举时一定要看能不能剪枝。换句话说,在填入数字的时候,就要考 虑三阶幻方的数值约束,不要等到最后再判断。这样做的好处是能够尽快排除 很多组合,比如:
● 我们尝试 a=9, b=8,这时 a+b 已经比 15 大,其他的 c, d, e, …, i 就不用 试了。
● 因为 a, b, c 之和为 15,只需要给定 a, b 的数值,即可推导出符合约束 的 c 的数值。比如 a = 9, b=1,可以推导出 c=6,不用再枚举 c 了。


代码下载及Web版
点击求解三阶幻方的代码下载于本地运行,或者点击三阶幻方Web版直接运行
国内用户如果无法访问scratch.mit.edu的话,请点击国内可访问的Web版直接运行
五、实验结果
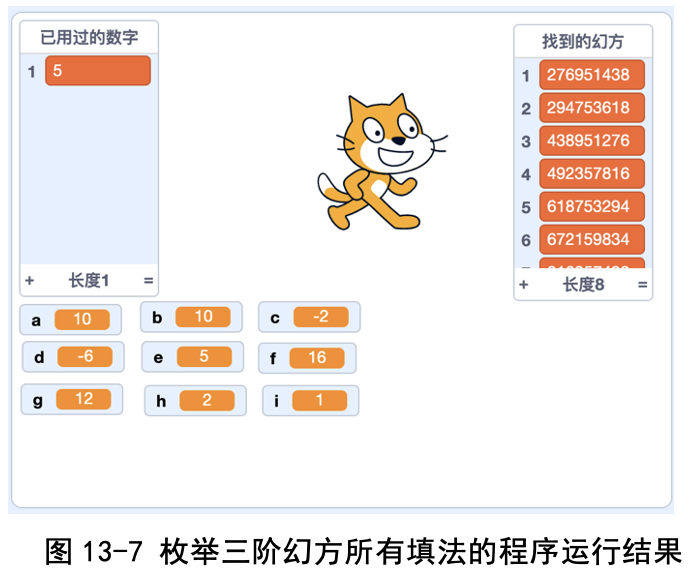
我们的程序运行得非常快,找到了 8 种幻方填法。
那这些结果对不对呢?我们手工枚举了一遍(用“包卜魏猜想”枚举很 快),和程序运行结果完全一致。我们也实现了笨方法和聪明的方法,这两种 方法的结果是一样的,只是聪明的方法判断次数少得多(见图 13-7)。
六、思考与延伸
三阶幻方我们会做了,那五阶幻方怎么做呢?道理是类似的,我们扩展一 下“包卜魏猜想”,五阶幻方可以很快地枚举出来。
七、教师点评
这堂课的重点和“数字谜”问题一样,还是“枚举时一定要注意剪枝”。
孩子们自己发现了“包卜魏猜想”,非常兴奋!学数学以及做数学研究时 (甚至不限于数学)形式猜想是一个很重要的步骤。写的这个程序也是完全依 赖于“包卜魏猜想”进行剪枝,因此写程序时热情高涨,这很好!