第12讲 聪明的枚举:巧解数字谜
一、实验目的
我们常常遇到这样的“数字填空题”:选择 1~9 中的数字填入空格,每个 格子填一个数字,使得等式成立。下面是一个例子。
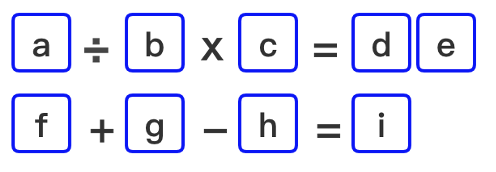
注意:这里我们不允许数字重复使用,也就是 1~9 这 9 个数,每个数都 只能用一次。今天咱们编个程序求解这道题吧。
二、背景知识
(一)最笨的方法怎么填?
老师一再告诉我们:碰到问题,先从最简单的,或者说最笨的方法开始, 再观察规律,根据观察到的规律逐步改进。
对于数字谜问题来说,最笨的方法就是“挨个试”:先试着把 a 填成 1, 把 b 填成 2,c 填成 3,d 填成 4,e 填成 5,f 填成 6,g 填成 7,h 填成 8,i 填 成 9。如果成立,那我们就胜利了;如果不成立,我们接着尝试其他填法。
这种方法叫作“枚举法”。顾名思义,就是把所有可能的填法都列举出来尝试一下,检验是否能够使等式成立。
(二)如何使得枚举时不遗漏可能的填数方案?
使用枚举法时最容易犯的错误就是遗漏一些可能的填数方案。要想不遗漏 的话,最好的方式是“画图”:先画一个点表示 a,然后从这个点开始分支,a 能填几个数,就分几支。以咱们这个问题为例,a 能填 1, 2, 3, …, 9,所以就 分 9 支。
接下来,针对 a 的每一种取值(就是每一个分支)继续尝试填 b,因为 b 能从1, 2, 3,…, 9中选,也有9种选择,我们就接着分9支。对c, d, …, i这些 数以此类推。这样我们就能把所有可能的填空方案都画出来了,还不会遗漏, 很好吧?
我手工画了一下这个图:每多考虑一个变量就长高一层,每一层又分 9 支。 这个图称为“树”,真的很形象,就是一棵倒着长的树啊!
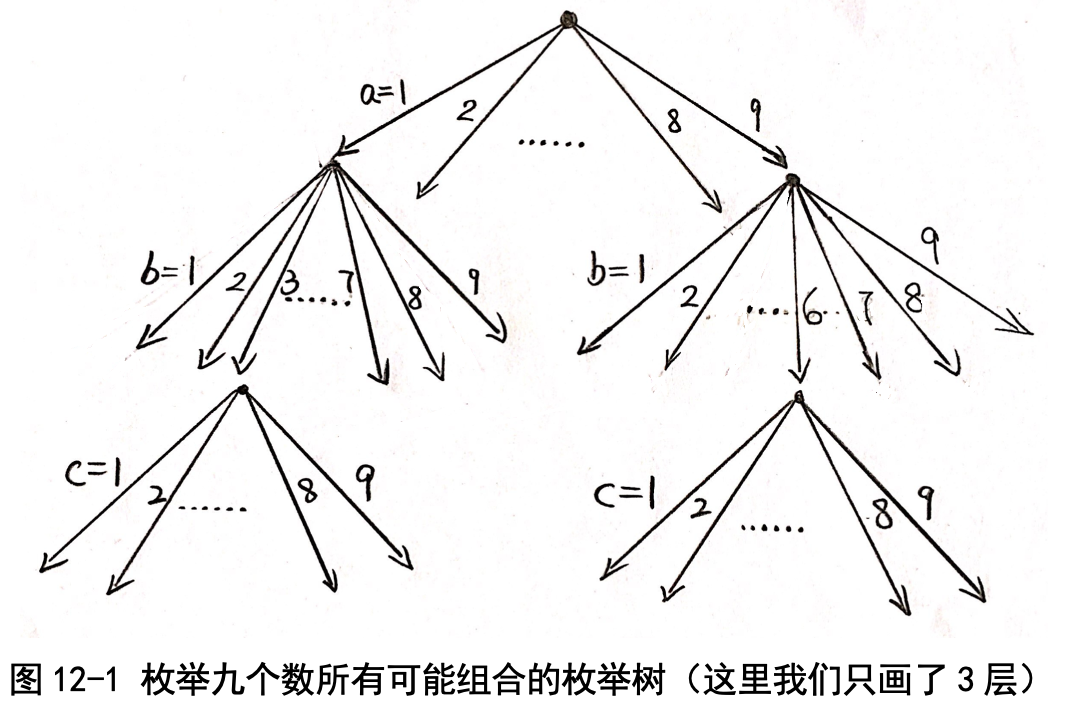
这个搜索树对 a, b, …, i 这 9 个变量进行分支,我只画了三层,看起来就 已经很多了。怎么办呢?一个聪明的方法是“剪掉一些不可能的分支”,这样 的话树就会大大“瘦身”,计算就很快啦!
(三)如何手工计算判断次数?
每个变量所有可能取值个数的乘积就是判断次数。这是因为每个变量的取 值变化一次,就会变成一个新的算式,判断次数就会加 1。举个例子,如果我 们用最笨的算法,每个变量都有 9 种可能,那么判断次数就是 9×9×…×9, 连乘 9 次,也就是进行 387420489 次判断。
三、基本思路
(一)最笨的枚举法
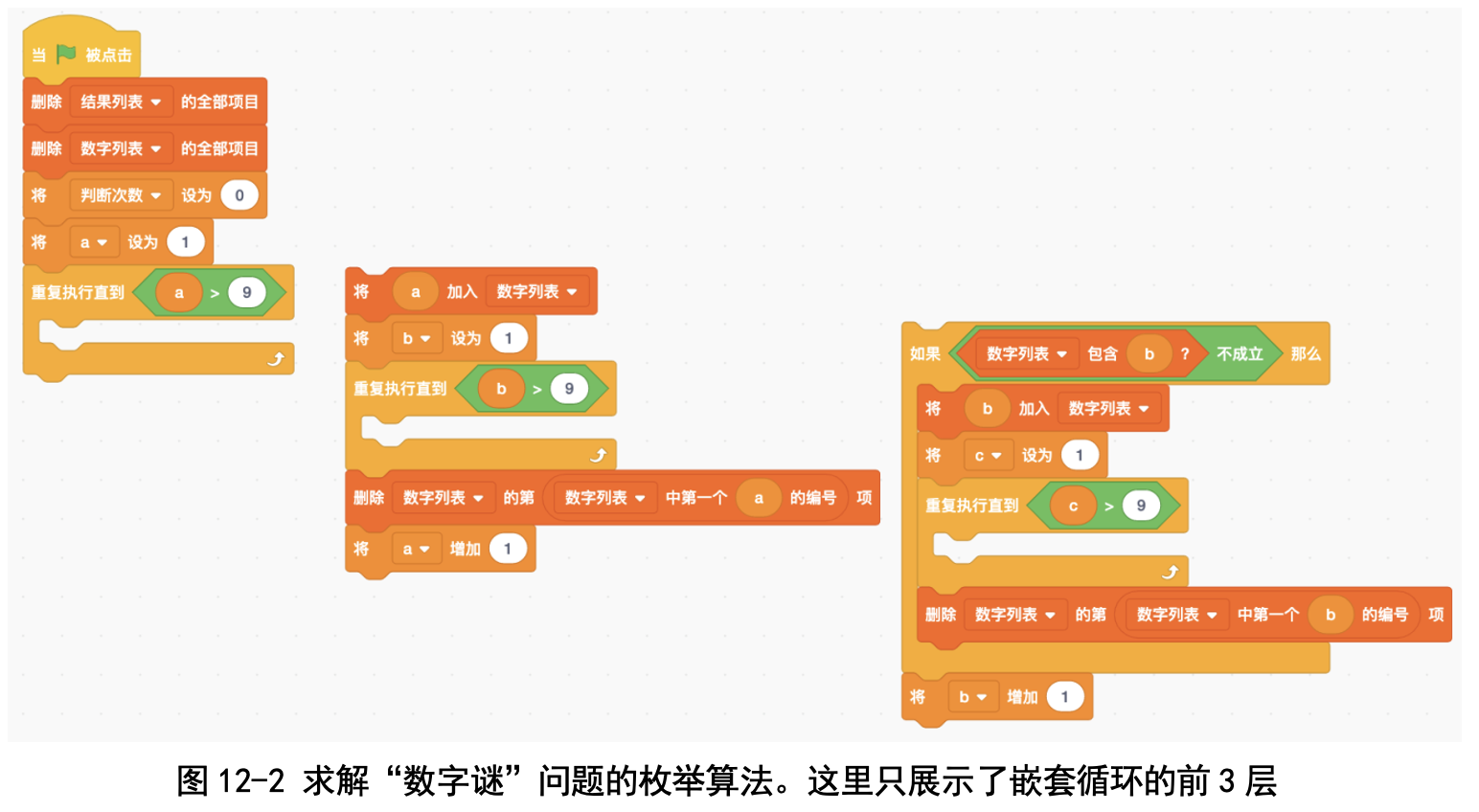
让 a, b, …, i 每个变量的取值都从 1 循环到 9,一共有 9 个变量,所以 要写一个 9 重的循环。当所有变量都确定取值之后,我们检验一下等式是否 成立。
(二)聪明一点的枚举法
我们自己发现了一个规律,可以用来减少判断次数。第 1 个变量 a 有 9 个 选择,第 2 个变量 b 不能和 a 重复,因此只有 8 个选择,类似地,第 3 个变量 c 有 7 个选择……第 9 个变量 i 只有 1 个选择。
画图看得更清楚:搜索树的第 1 层有 9 个枝杈,第 2 层有 8 个枝杈,第 3 层有 7 个枝杈……,最后一层只有 1 个选择,就可以直接判断了,所以总共有 9×8×7×6×5×4×3×2×1 条路径,也就是进行 362880 次判断,这可比刚 才的笨方法简便多了!
(三)更聪明的枚举法
我们自己又发现一个规律:当知道 a, b, c 的取值之后,可以算出 d, e 来,因此不用枚举 d, e 的取值。类似地,当知道 f, g, h 的取值之后,可以计算出 i 来,因此也不用枚举 i 的取值。
这样,我们只用枚举 a, b, c, f, g, h 这 6 个变量就可以了。也就是说,最多 只需要进行 9×8×7×6×5×4=60480 次判断就可以了。 事实上还有一些规律,用了这些规律之后,最聪明的算法只需要进行 96 次判断就能得出结果了。
小朋友们,你也试试吧?
提示一下,第一个式子算出 的结果必须是一个两位数,第二个式子算出的结果必须是一个一位数。利用这 两个性质进行排除,判断次数还会大大减少。

代码下载及Web版
点击求解数字谜的代码(聪明很多的算法)下载于本地运行,或点击求解数字谜Web版直接运行
国内用户如果无法访问scratch.mit.edu的话,请点击国内可访问的Web版直接运行
点击求解数字谜二的代码(聪明的算法)下载于本地运行,或点击数字谜二的Web版直接运行
国内用户如果无法访问scratch.mit.edu的话,请点击国内可访问的Web版直接运行
六、实验结果
(一)算法找到多少种答案?
如图 12-4 所示,不管是用笨办法还是聪明的办法,最终找到的答案都是 一样的— 96 种答案(因为两个算式组成一种答案,所以共有 192 个算式)。
(二)对比笨算法和聪明算法的判断次数
超级笨办法的判断次数是 387420489(天啊,要算这么多次),聪明一点的算法的判断次数是 362881 次(见图 12-4),而最聪明的算法只需要判断 96 次 (见图 12-5)!“刷”的一下就运行结束!不同算法的差别真大呀!


七、思考与延伸
在上课时,我们想起来那个“算 24”的游戏,就是给定 4 个数,用加减 乘除运算(允许带括号)算出 24 来。我们把这个程序改动一下,加上数字的 换位就可以了。
写完这个程序之后,我们又写了一个程序,解一个新的数字谜:将数字 0, 1, 3, 4, 5, 6 填入空格,每个数字只能使用 1 次,使得下面这个等式成立。小朋 友们,你们也试试吧!
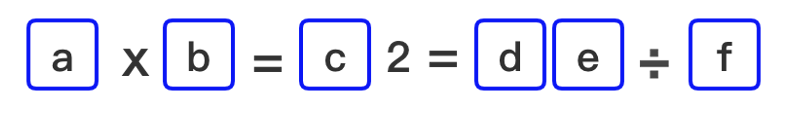
八、教师点评
“数字谜”是常见的小游戏,可以采用“枚举”策略来解决。同学们通过 嵌套的循环,领会了基于枚举策略的求解方法。
枚举的关键是“剪枝”,就是尽量减少不必要的分支。比如在这个题目里, d, e 和 i 这 3 个变量可以直接确定,不需要枚举。对比带剪枝的和不带剪枝的 算法,孩子们对剪枝的威力印象深刻!
对这个题目,我们是从先实现最笨的方法开始,观察到规律就改进一下, 再观察到规律再改进一下。孩子们也领会到了“不能一口吃个胖子”,要“逐 步优化”。
枚举过程中一定要注意剪枝,那怎样进行剪枝呢?
兰老师讲过一个很有效的策略,叫“找突破口”,就是说通过分析和推理, 能够排除一些变量的取值。
拿“思考与延伸”里的那个数字谜为例,有 a, b, c, d, e, f 六个变量,为什么分支的时候一定要从 a 开始呢?先考虑哪一个变量结 果都是一样的,要是先考虑取值范围少的变量,枚举会更简单。
我们可以这样分析:
第一步:找一个突破口。
我们来看 a×b=c2 这个等式。两个数乘积的个位数怎样才能变成“2”呢?枚举一下发现这两个数的组合只能是 1×2,2×1,3×4,4×3,2×6, 6×2 这几种。不过因为 2 不能用,所以只能是 3×4 或 4×3。3×4=4×3=12 说明 c 只能等于 1。a 等于 3,b 等于 4 或者 a 等于 4,b 等于 3。 用 a×b=c2 这个等式,一下子能够排除很多组合,所以这个等式是一个很 好的“突破口”。
第二步:根据 de÷f=12 这个等式,我们可以推断出 e 只能是 0。
原因很简单:f 是除数,所以不能是 0;d 出现在十位上,也不能是 0。 如果 d 是 5,那么 f 就是 6,但是 50÷6=12 不成立,因此只剩下一种可能 性了:d 是 6,f 是 5,60÷5=12,等式成立。 第三步:连接上面两个等式,得到下面两种填法:
第一种:3×4=60÷5=12
第二种:4×3=60÷5=12
这种“找突破口”策略很灵:我们只需要考虑 2×1×1×1×1×1×1=2 种 组合,比笨的枚举法快多了!
我们结合奥数课的内容设计了这次练习。孩子们发现笨方法考虑的填法太 多了,单靠手工计算是很难完成的,只有写程序才能完成,而聪明的方法只看 几步就行了。“枚举一定要注意剪枝,剪枝的关键是找准突破口,先考虑那些 选择范围少的变量”,这是我们想让孩子们领会的计算思维之一。