第11讲 逐级逼近法:刘徽割圆法估计π
一、实验目的
今天是2020年3月14日,是“数学节”。之所以这天被选中作为数学节, 是因为“3.14”是圆周率π的前 3 位数字,而π非常重要,足以代表数学。
今天,我们就编程计算一下π的值吧。
二、背景知识
(1) π 是什么?
我们从小学三年级就知道 π 就是圆周率,就是“圆的周长 ÷ 直径”。周 长,顾名思义,就是圆的一周的长度;而直径呢,就是先画一条直线穿过圆 心,和圆相交的两个点之间的线段的长度就是直径了。
(2) π 是多少?
古代人说“周三径一”,意思是说一个圆的直径是1尺时,周长就是3尺, 换句话说,古时计算的圆周率 π 等于 3。
我自己找了一枚圆圆的硬币,用尺子量了一下直径,是 2.8cm ;又用了一 根线绕圆一周,量量长度,周长是 9.0cm ;通过计算两者之比,我估计出圆周率是 π≈9.0÷2.8≈3.21(见图 11-1)。当然了,这是很粗糙的估计;现在人们 已经算得非常精确了:π=3.1415926…,是一个无穷无尽、写也写不完的数, 还不会出现循环。

一个数无穷无尽还不重复,这很奇怪;我们现在上四年级,见到的小数要么是 有限长度的,比如 1÷2=0.5,小数点后只有一位数字;要么是无限循环小数,比 如 1÷3=0.333…,虽然是无穷无尽的,可是小数部分一直是 3,是一个循环小数。
像 π 这样有无限位数又不循环的小数,真的很奇怪;老师告诉我们,这叫 “无理数”。老师还特意强调:这里的“理”不是“道理”的意思,而是“比例” 的意思;无理数不是“没有道理的数”,而是“不能表示成两数之比的数”。初 学者往往会望文生义,现在就得纠正。
怎样找一个数尽量接近 π ?
π 太复杂了,那能不能找一个数与之近似呢?我国南北朝时期(比唐朝还早) 的大数学家祖冲之找到了两个数,都跟 π 很接近,一个叫约率,另一个叫密 率。老师提醒我们说:“这两个数都是有理数,祖冲之是用有理数近似无理数。”
……
(4) 刘徽割圆法估计 π
那祖冲之是怎样得到 π 的近似值的呢?
这个还缺乏明确的历史文献佐证。不过研究数学史的人猜测祖冲之是采用 “刘徽割圆法”估计出 π 的。今天我们就用刘徽割圆法算一算 π 吧!
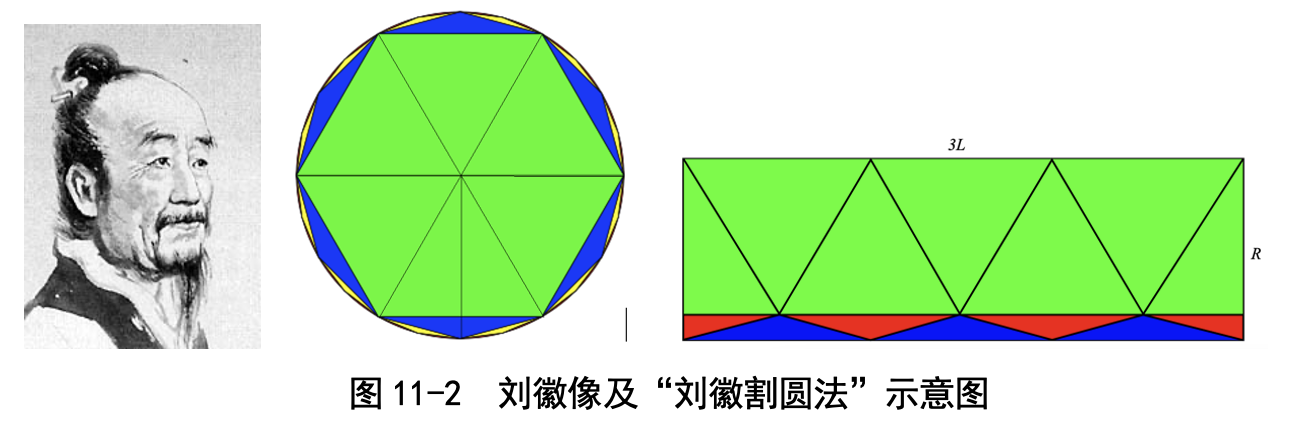
刘徽割圆法非常好理解:圆的周长不好算,但是多边形的周长好算啊,咱 们就用多边形的周长代替圆的周长吧。比如图 11-2 中的六边形(绿色的),看 起来有点像圆了,不过还有一点差别,咱们就再多一点儿,用十二边形(蓝色 的),就更像圆了。再多一点儿,用二十四边形(黄色的),就跟圆非常像了。 老师提醒我们,这里的六边形是“正六边形”,就是各条边的长度都相等。据 考证,刘徽用正 96 边形估计出 π 等于 3.1416。
这个方法很直观,我也想到了这个“逐渐逼近圆”的方法:从三角形开始,四 边形,五边形,……,逐渐增加,不断逼近圆,越来越像圆。卜老师告诉我们,大 家发现了正多边形不断逼近圆,这个发现反过来说,就是圆是正多边形的极限。
想出这个方法的时候,我兴奋极了。后来才知道刘徽早在三国时期(约 1800 年前)就知道了。说起三国,我过去只会想起刘备、关羽、张飞和诸葛 亮,现在我还会想起刘徽。
……
详细内容请阅读书的第11讲。
三、基本思路
想用刘徽割圆法算出 π,第一步得画出正多边形,第二步得计算正多边形 的周长。我们一步一步来吧。
(1) 画正多边形
要画正多边形的话,我们得先把顶点定下来。那怎样确定顶点呢?
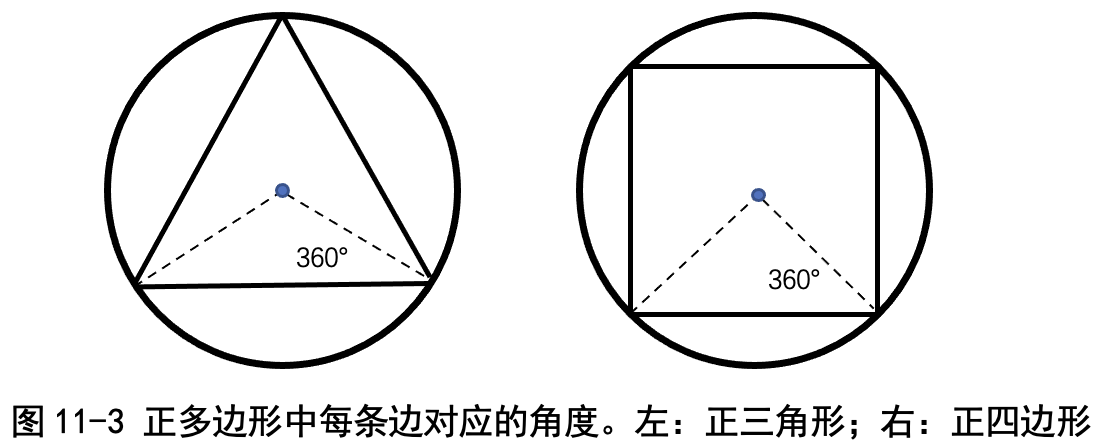
咱们从最简单的做起吧。先看正三角形(也常称作等边三角形):绕圆一周 会旋转 360°,那三角形的一条边应该对应 360÷3=120° ;所以,我们从原 点出发,沿着 0°方向走半径那么远,就会到达第一个顶点;再回到原点,从 原点出发,沿着 120°方向走半径那么远,就会到达第二个顶点;从原点出发, 沿着 240°方向走半径那么远,就会到达第三个顶点(见图 11-3)。
类似地,要画正四边形的话,一条边应该对应 360÷4=90°,因此只要沿 着 0°,90°,180°,270°走半径那么远,就能把 4 个顶点确定下来了。
看完这两个例子,我们对一般的正多边形也会画了:假如边数是 n,我们 就先计算 360÷n 是多少度,然后从 0°开始,每次增加 360÷n 度,从原点出 发走半径那么远,就到达顶点了。
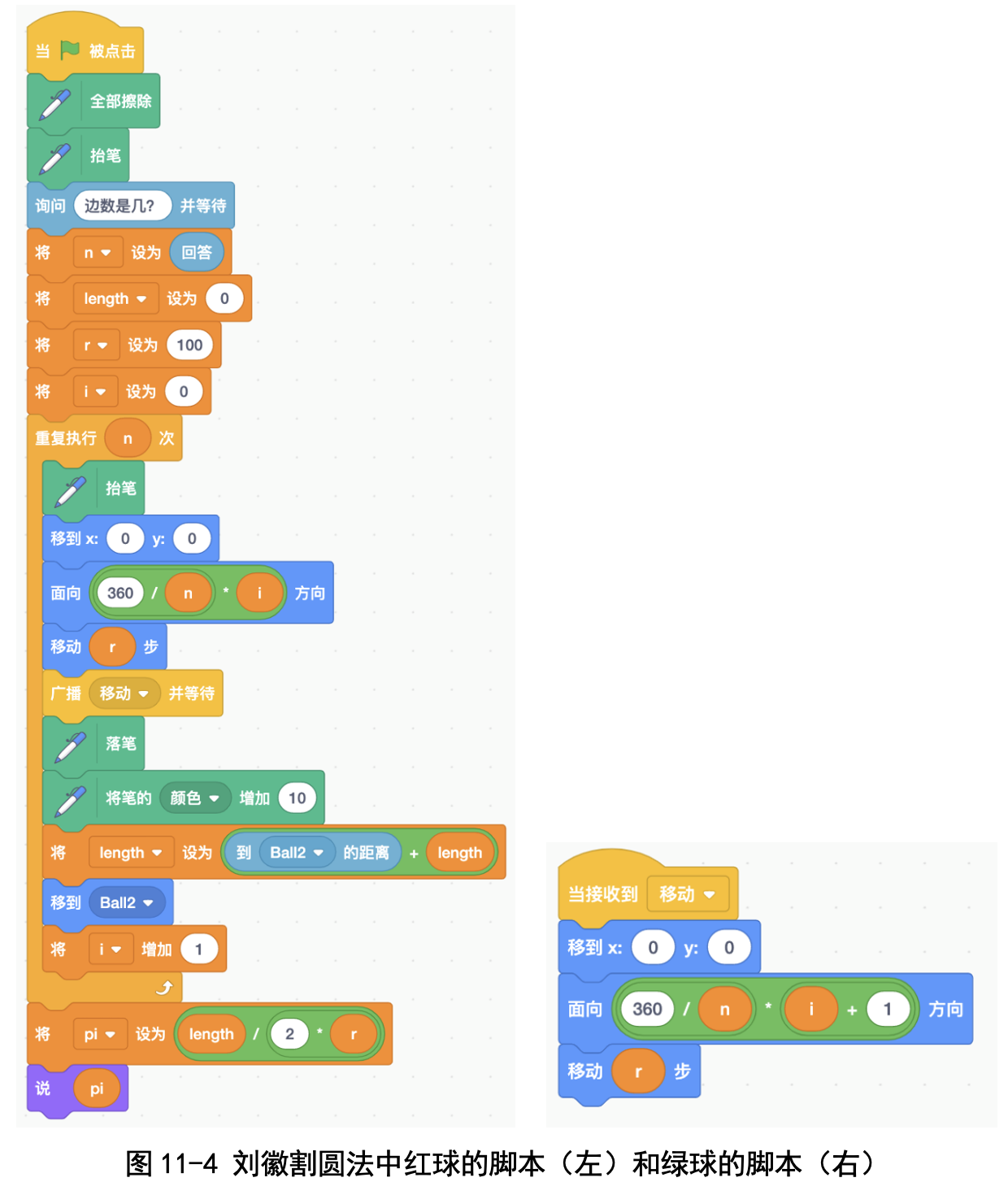
在确定了顶点之后,画多边形就容易了:我们利用 Scratch 的画笔功能, 从第一个顶点走到第二个顶点,就能把第一条边画出来;从第二个顶点走到第 三个顶点,就能把第二条边画出来;其他的边依次类推。
(2) 计算正多边形的边长
这个比较简单:Scratch 里“侦测”栏里有一个“到鼠标指针的距离”积木: 我们把“鼠标指针”改成一个角色,就能得到两个角色之间的距离。比如,我 们设置两个角色,让角色 1 走到第一个顶点,让角色 2 走到第二个顶点,然后 让角色 2 计算“到角色 1 的距离”,就能够得到两个顶点之间的距离了。把所 有边的长度累加起来,就能得到多边形的周长了。
代码下载及Web版
点击刘徽割圆法的代码下载于本地运行,或点击刘徽割圆法Web版直接运行
国内用户如果无法访问scratch.mit.edu的话,请点击国内可访问的Web版直接运行
六、实验结果
(一)随着正多边形边数(n)的增加,π 的估计值的变化
(1)三角形,n=3,π 的估计值为 2.598076。
(2)正方形,n=4,π 的估计值为 2.828427。
(3)正五边形,n=5,π 的估计值为 2.938926。
(4)正六边形,n=6,π 的估计值为 3。
(5)正一百边形,n=100,π 的估计值为 3.141076。
(6)正一万边形,n=10 000,π 的估计值为 3.141593。
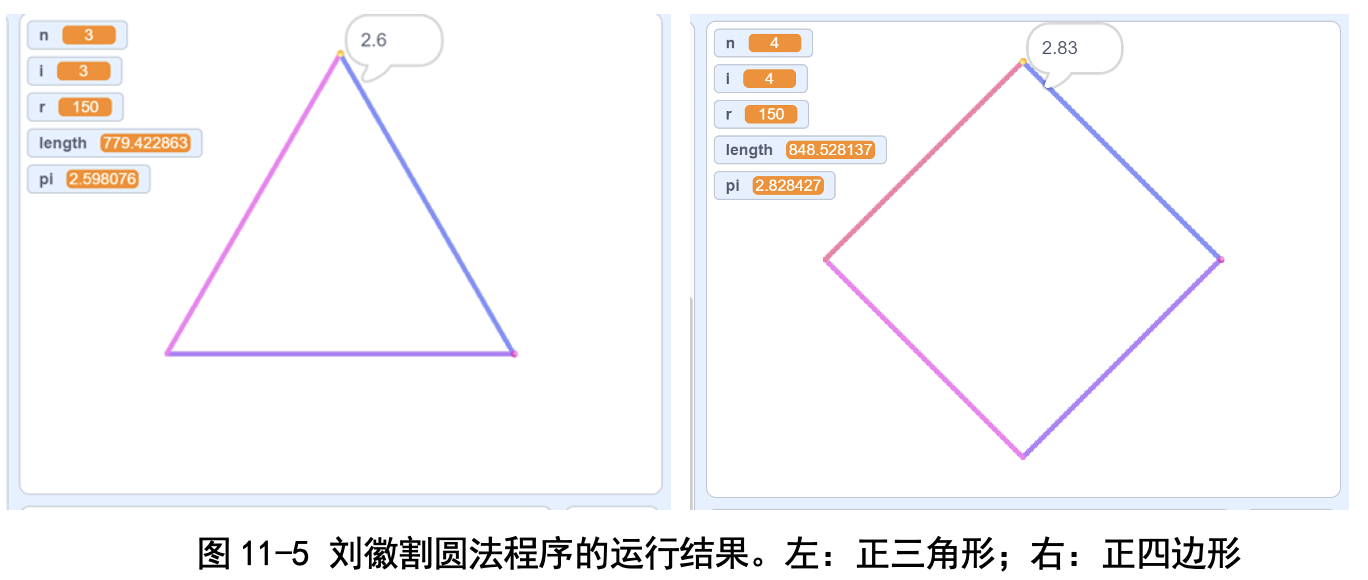
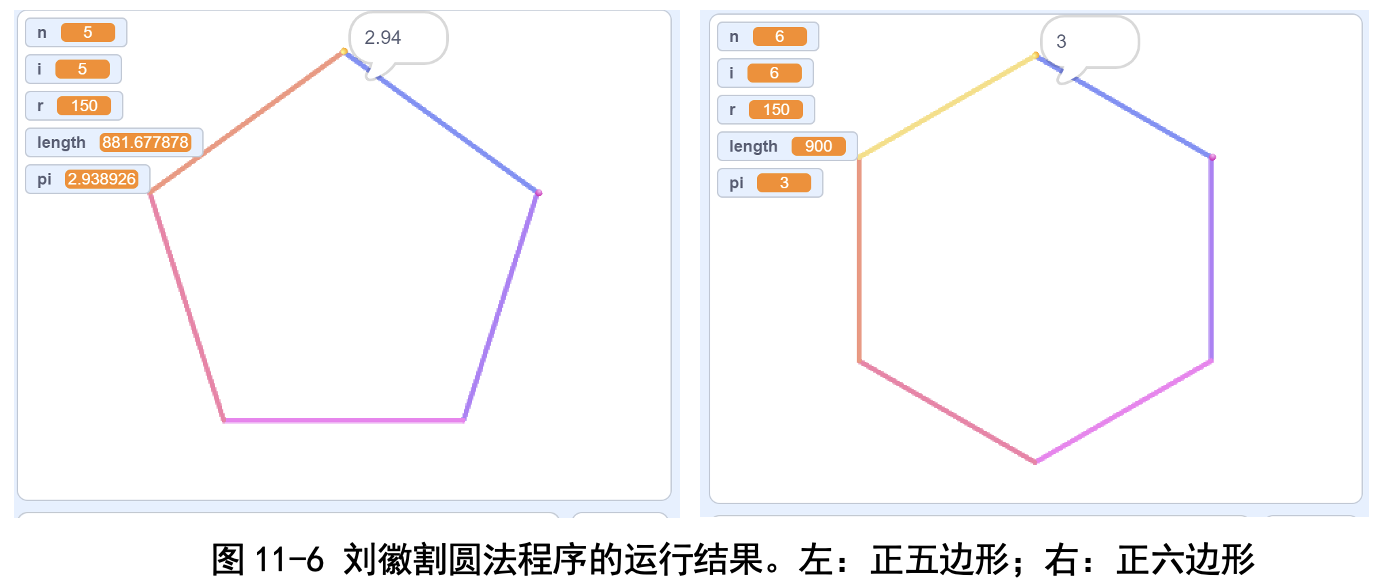

如图 11-5~图 11-7 所示,随着正多边形边数的增加,得到的图形越来越 像圆了,估计出的圆周率也来越准。后面就不介绍了,因为后面得出的全部都 是 3.141593 这个值。
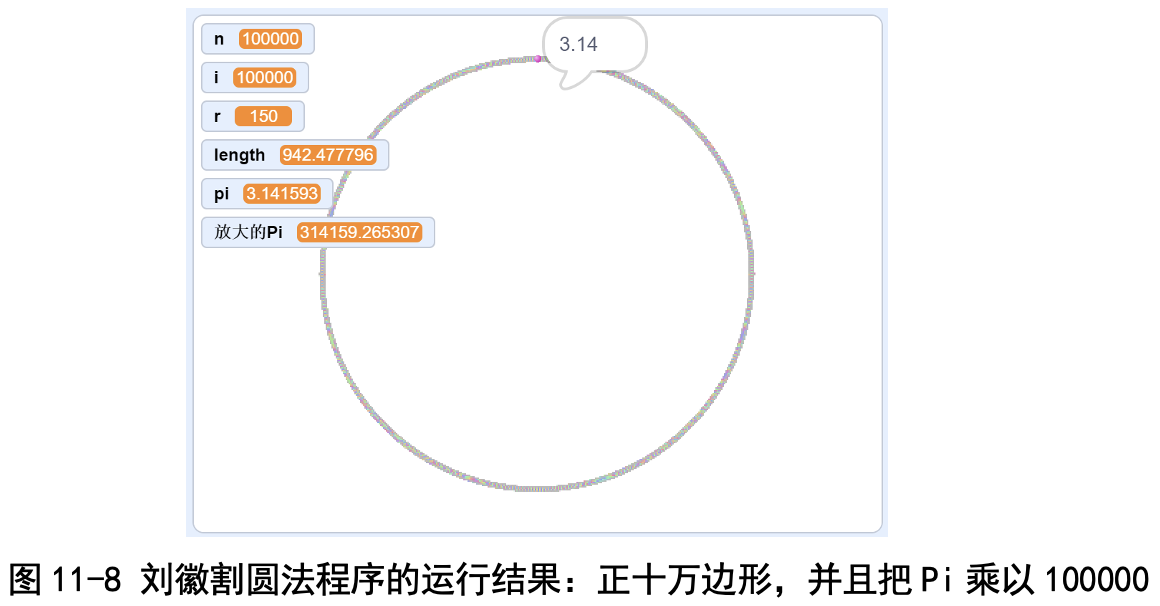
为什么边数再增加,程序算出来都始终是 3.141593,不再更新了呢?老师 告诉我们,这是因为 Scratch 算边长的时候,小数点后只能显示 6 位数字。于 是我们想了个办法:把结果 pi 乘以 100000,得到 314159.265307(见图 11-8), 这样就又精确了 4 位小数“2653”。
(二)大圆小圆的结果一样吗?
网上的资料说,刘徽当年是用半径 1 尺的圆计算圆周率的。这里我改变了 半径,一个是半径为 150 的大圆,另一个是半径为 100 的小圆,我们看一看大 圆小圆计算出的结果是否一致,得到的结果如图 11-9 所示。
我发现不管是大圆还是小圆,算出来的结果都是 3.14076,基本上是一 样的。

七、教师点评
π 是非常重要的数。孩子们在 3 月 14 日这一天,通过编程自己亲手把 π 算出来,这很有意义。
用多边形近似圆,孩子们自己(比如卜文远同学)也有这个朦胧的想法; 最后画出来的正一万边形、正十万边形越来越像圆,估计出的 π 越来越精确, 孩子们非常兴奋!
当然了,本章的估计方法没有用到刘徽割圆法的“迭代”过程,这是一个 缺陷,这也是受限于小学生的知识储备,不得不做出的让步。
除了编程实现之外,我们还给孩子们补充了如下知识:
(一)为何叫“割圆法”?哪里体现了“割”?
以正六边形为例,割圆法就是把圆分割成 6 份,用 6 个小三角形近似圆。
刘徽割圆法的核心之一在于“正多边形面积的迭代计算方法”,是讲怎样 “根据正 n 边形边长计算正 2n 边形的面积”。刘徽的原话是“以六觚之一面乘 半径,因而三之,得十二觚之幂;若又割之,次以十二觚之一面乘半径,因而 六之,则得二十四觚之幂”,也就是:
正十二边形的面积 = 正六边形边长 ×3× 半径
正二十四边形的面积 = 正十二边形边长 ×6× 半径
其中的道理很简单:你看图 11-2,正十二边形就是正六边形外加 6 个小三角 形;为了求正十二边形的面积,刘徽先把正六边形切成 6 个大三角形,摆放成类似 长方形的样子,再补上那 6 个小三角形,就得到一个完美的长方形了(长方形中有 一个小三角形被分开显示了)。这个长方形的长是正 6 边形边长 ×3,宽是半径。
刘徽割圆法使用勾股定理,先计算正十二边形的边长,然后计算出正 二十四边形的面积,再应用勾股定理计算正二十四边形的边长,进而计算出正 四十八边形的面积。这样由边长算面积,再由面积算边长,不断进行,就能不 断逼近圆的面积了。
(二)本讲采用的方法与刘徽割圆法的差异
(1)刘徽割圆法是“用多边形的面积逼近圆的面积”,我们这里为了便于 编程实现,没用面积,而是使用“多边形的周长逼近圆的周长”。
(2)用面积的好处是可以“两侧逼近”,即刘徽使用内接正多边形,面积 始终比圆的面积小,同时在这个正多边形外边附加了一些矩形,总面积比圆的 面积大,这样同时算出两个数,一个比 π 大,另一个比 π 小。
我们这里只用了内接正多边形的周长,只做到了单侧逼近,即算出来的这 个数虽然接近 π,但始终比 π 小。做两侧逼近,需要用到勾股定理,我们留给 高年级的小朋友们思考和尝试。
(3)刘徽是从正六边形开始,每次倍增,作正十二边形、正二十四边形 等。我们这里用的是正三边形、正四边形、正五边形等,这个影响其实不大。 历史上,赵友钦割圆法也是用的正四边形。
(三)刘徽和祖冲之的生平
刘徽是淄乡(今山东邹平市)人,生活在三国和魏晋时期;他为《九章算 术》做注,提出用割圆术计算圆周率的方法。刘徽的名言“割之弥细,所失弥 少,割之又割以至于不可割,则与圆合体而无所失矣”,精辟地描述了割圆法 的迭代过程。
祖冲之,字文远(卜文远知道后非常兴奋), 出生于建康(江苏南京), 是南北朝时期人,比刘徽小大约 200 岁。他在刘徽割圆法的基础上继续改进,首 次将圆周率精确到七位数字,即在 3.1415926 和 3.1415927 之间。
最后再补充一点:古时候还没有小数点,小数是用分数来表示的。古人在 没有现代便利的阿拉伯数字表示方式的情况下还能算得这么精确,真是值得 钦佩!